Warum ist das Schöne schön? (Teil IV)

Die Entdeckung der geometrischen Ursachen der musikalischen Harmonie von Pythagoras und Kepler

IV. Teil: Kepler als Wegbereiter der Wohltemperierung

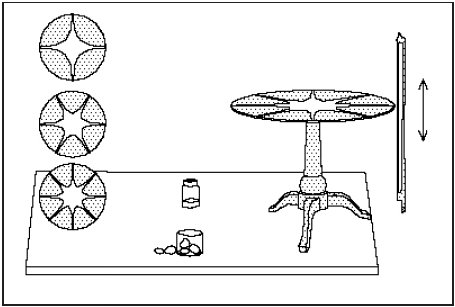
Ernst Chladni (1756-1827, oben) war eigentlich Doktor der Philosophie und der Rechte zu Wittenberg und veröffentlichte im Jahre 1787 seine Forschungsergebnisse in der Schrift "Entdeckungen über die Theorie des Klanges". Darin begründete er die experimentelle Akustik und entdeckte die nach ihm benannten "Chladnischen Klangfiguren". Mit einem Geigenbogen strich er an der Kante einer Platte entlang (Bild unten), die mit Sand bestreut war. Auf der schwingenden Metallplatte verteilte sich der Sand, und es entstanden schöne geometrische Muster, mit denen Chladni Schwingungsvorgänge sichtbar machen konnte.

In der letzten Folge haben wir Keplers Begründung der "Konsonanz" durch eine bestimmt definierte, ausgewählte Zahl von Kreisteilungen kennengelernt. Diese Erklärung der konsonanten Schwingungsverhältnisse als wahre Erscheinung der Natur wurde von Ernst F. Chladni - dem Lehrer der Brüder Weber, der ein bedeutendes Werk über die "Akustik" verfaßte und auch wie Benjamin Franklin Glasharmonikas baute - im frühen 19. Jh. nachgewiesen. Chladni führte ein erstaunliches Experiment durch, indem er Glasplatten mit Sand bestreute und dadurch in Schwingung versetzte, indem er sie mit einem Geigenbogen an der Kante anstrich. Wenn die Platten zu einem Ton angeregt wurden, so sprang der Sand an bestimmten Stellen hoch und an anderen blieb er liegen. Dadurch formten sich auf den Platten Vielecke, je nach Schwingung Dreiecke, Vierecke, Sechsecke oder Achtecke! (siehe Abb. 1).

Es stellen sich nun die folgenden Fragen:

Erstens: wie baute Kepler die Tonleitern auf, wie ermittelte er also die Schritte zwischen den Tönen, den Ganzton oder Halbton? Dabei werden wir sehen, daß er diese ganz systematisch ebenfalls als Ergebnis bestimmter Kreisteilungen herleitet, wobei er die Tatsache erklärt, warum es verschieden große Halbton- und Ganztonschritte gibt.

Zweitens: was schlug er den Instrumentalisten als Stimmungsmethode vor? Die verbreiteten Instrumente der damaligen Zeit - vor allem die Laute - besaßen eine bestimmte, durch die Unterteilung der Saiten festgelegte Anzahl von Tönen. Bei den Orgeln sind ja die Töne durch die Tasten festgelegt. Nur bei den Instrumenten der Geigenfamilie (Violine, Viola, Cello und Kontrabaß), deren Griffbretter keine Bünde besitzen, kann man die Töne frei wählen wie bei der menschlichen Stimme. Die ersten Violinen tauchen aber erst ca. 1518 in Zeichnungen Dürers auf.

Betrachten wir zuerst seine weiteren Entdeckungen über die Intervalle: Aus der Geometrie ergibt sich erst einmal ein Unterschied zwischen den verschiedenen Konsonanzen, die kleiner sind als das Verhältnis 1:2, und die daraus entstehenden Intervalle sind nur vier, welche er die "melodischen" nennt. Diese entstehen also rein aus der Natur der Harmonik:

"Obwohl ferner auch die konsonanten Intervalle verwandte Ursachen haben, so haben doch nicht alle die gleiche, sondern jedes hat seine besondere, von denen der übrigen verschiedene Ursache, wie wir oben gezeigt haben. Denn die Konsonanz kommt den Intervallen zu, nicht insofern diese einfach soundso groß sind, auch nicht insofern als sie einfach Relationen sind, sondern insofern sie qualitative (d.h. gewissermaßen figürliche) Relationen sind... und es stimmt mit dem früher Gesagten ... wohl überein, wenn jedes dieser der Natur nach melodischen Intervalle die Natur der konsonanten Intervalle beibehält, aus denen es gebildet wird. Da nun unter den konsonanten Intervallen, die kleiner sind als das doppelte, die vollkommensten Intervalle 2/3 und 3/4 sind wegen des ausgezeichneten Rangs der Figuren, von denen sie ihren Ursprung herleiten, wird man auch deren gemeinsamen Abkömmling 8/9 den übrigen melodischen Intervallen vorziehen müssen."¹

Aus dem Vergleich der Quinte (2:3) und der Quarte (3:4) entsteht nämlich das melodische Intervall 8:9, welches er "in Übereinstimmung mit den Alten" den vollkommenen größeren Ganzton nennt.

Es ergibt nämlich:

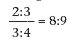
Notenbeispiele für den großen Ganzton 8:9 sind z.B. die Tonschritte g - a sowie c - d (siehe Abb. 2 a).

"Wenn man weiter das größere vollkommene Intervall 2/3 mit dem größeren unvollkommenen, höheren Intervall 3/5, oder das kleinere 3/4 der vollkommenen mit dem kleineren, niedrigeren 5/6 der unvollkommenen Intervalle vergleicht, entsteht aus dieser Verbindung das unvollkommenere melodische Intervall 9/10, das kleiner ist als 8/9. Während dieses Intervall in der alten Musik vor Ptolemäus fast nicht bemerkt worden ist, insofern die Theoretiker alles durch die vorhin definierten Ganztöne darstellten, wollen wir ihm den Namen kleinerer oder "kleiner Ganzton" geben, um damit seine Unvollkommenheit zu bezeichnen."²

Der "kleine Ganzton" entsteht aus dem Vergleich zwischen Quinte und großer Sexte, aber auch dem zwischen Quarte und kleiner Terz:

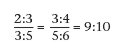
Beispiele für diese kleinen Ganztöne sind die Intervalle a - h, d - e oder f - g (siehe Abb. 2 b).

Kepler zeigt außerdem den Unterschied zwischen einem kleinen und großen Halbton - dem "Limma" 80:81, etwa zwischen dem Schritt g - a (großer Ganzton 8:9) und dem Schritt a - h (kleiner Ganzton 9:10) - , welchen das Ohr nur "mit dem Verstande" wahrnimmt, wenn man gleichzeitig die Saiten der Länge 80 sowie 81 ertönen läßt.

Der Halbton 15:16 entsteht, wenn man die Quinte 2:3 mit der kleinen Sexte 5:8, oder die Quarte 3:4 mit der großen Terz 4:5 vergleicht:

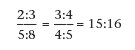
Notenbeispiele für den Halbton sind die Schritte h - c oder cis - d (siehe Abb. 2 c).

Kepler nennt nun noch ein viertes Intervall, das er aber aus einem bestimmten Grund nicht mehr zu den "melodischen" zählen will: das Verhältnis 24:25, welches aus dem Vergleich der großen und kleinen Terzen untereinander sowie dem der großen und kleinen Sexten untereinander entsteht:

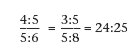
Beispiele aus der Musik sind die Schritte: dis - e; f - fis oder b - h (siehe Abb. 2 d).

Er zählt es lieber zu den "Intervallen dritter Art" und nennt es "Diesis", doch betont er, daß er damit nicht das gleiche Intervall meint, welches die Pythagoräer Diesis nannten. Seine Unvollkommenheit wird nun folgendermaßen begründet, womit Kepler uns in die charakteristischen Merkmale einer jeden Tonart und die Probleme der "Temperierung" einführt: Erstens ist es unvollkommen, weil es aus den unvollkommeneren konsonanten Intervallen - den aus Fünfeck oder Zehneck entstandenen - gebildet ist, also 4:5 und 3:5; aber auch wegen seiner Kleinheit, denn es ist noch nicht einmal so groß wie das Drittel eines Ganztons. Außerdem entsteht es auch, wenn man einen kleinen Ganzton mit dem Halbton vergleicht, also aus 9:10 und 15:16. Es gehört aber vor allem anderen zur "dritten Art der Intervalle", weil es zur "Erzeugung der Tongeschlechter dient":

"Dieses Intervall ist nicht an sich und nicht immer melodisch. Die menschliche Stimme liebt es nicht, den Gesang in einer und derselben Agoge [zwei direkt aufeinanderfolgende Töne, C.H.] durch dieses Intervall zu führen wie durch die übrigen Intervalle; sie verschmäht und überspringt es und verwendet es nur bei der Modulation, um einen besonderen Effekt zu erzielen. In diesem Fall wird es in außerordentlicher Weise melodisch, aber in der Weise, daß gewissermaßen eine neue Art von Gesang anhebt; auch gehört mehr als mittelmäßige Kunstfertigkeit und Anstrengung dazu, mit der menschlichen Stimme ohne Instrument dieses Intervall zu treffen. Es schafft daher nur eine Unterscheidung der Arten melodischer Intervalle und dient somit diesen."³

Das bedeutet also, daß man nur, wenn man die "Eigenart" der jeweiligen Tonleiter hervorhebt, d.h., ihren Charakter, der sich aus der eigentümlichen Verteilung der kleinen und großen Halb- und Ganztöne ergibt, bei der Modulation (dem Übergang von einer zu einer anderen Tonart) "eine neue Art von Gesang" erreicht. Wie aber sollte man dies auf Instrumenten schaffen?

Zur Zeit Keplers hatte man eine sehr mechanische, oder besser gesagt, "gleichmäßig proportionierte" Methode gefunden, Instrumente zu stimmen. Man meinte, ähnlich wie das in der heutigen Art der "gleichschwebenden Stimmung" gemacht wird, es den Instrumentalisten auf Kosten der Tonartcharakteristik einfacher machen zu können. Er beschreibt dies folgendermaßen:

"Freilich werden nach musikalischem Herkommen alle Intervalle ausgeglichen, so daß keines rein bleibt, und die Intervalle, die vollkommen sein sollten, durch eine kleine Einbuße an ihrer Vollkommenheit die Unvollkommenheit der übrigen verringern und mildern. Dadurch kommt es, daß alle Ganztöne auf den Instrumenten gleich sind; so ist auch das Limma gleich dem Halbton, und zwei Halbtöne machen infolge genauer Zweiteilung einen Ganzton aus..."⁴

Als Beispiel führt er eine Methode von Aristoxenos vor, die von Vincenzo Galilei, dem Vater Galileo Galileis, zur Stimmung von Lauten vorgeschlagen wurde: Man teilt die Saite der Laute vom Steg bis zum Saitenhalter in genau 18 Teile. Die erste Griffmarkierung ("Bund") bringt man von den Wirbeln ab so an, daß oben 1 Teil, unten 17 Teile liegen. Darauf zerlegt man die übrigen 17 Teile wiederum in 18 und bringt die zweite Griffmarkierung so an, daß man davon unten einen Teil abschneidet. Der Rest wird wieder in 18 Teile geteilt, und so macht man es zwölfmal hintereinander, so daß man jeweils einen Halbtonschritt markiert hat. Galilei behauptet, daß die restliche Saite genau die Hälfte der Ausgangslänge ausmacht, so daß zwischen Rest und ganzer Saite die Konsonanz einer Oktave besteht. Kepler rechnet das nun nach.

Er nimmt für die Länge der Saite der besseren Darstellung halber die Zahl 100,000 an, teilt die Strecke in 18 Teile und teilt 1/18 ab - und erhält 94,444. Nehmen wir einmal die Grundschwingung g an, so ist dies also das gis. Wenn man nun 94,444 wiederum in 18 Teile teilt, erhält man 89,198 an der Stelle, wo man das a markiert. Und so fährt man fort, indem man den Rest insgesamt 12 mal in 18 Teile teilt (siehe Tabelle 1):⁵

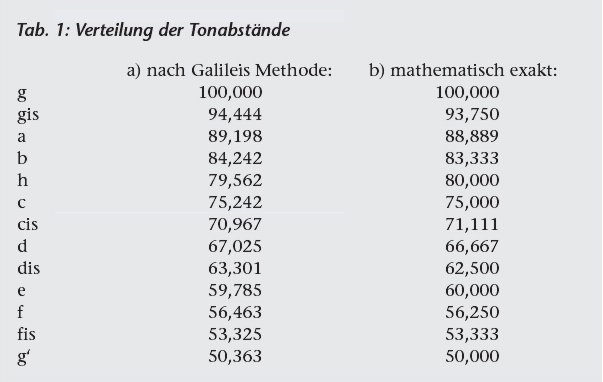
Kepler hat einen Einwand gegen Galileis mechanische Methode:

"Wäre dieses Verfahren genau richtig, so wäre die Proportion, die sich nach zwölfmaliger Wiederholung ergibt, gleich dem Verhältnis 1:2. Gute Mathematiker wissen aber, daß diese Annahme falsch ist, da 1/2 und 17/18 inkommensurabel sind. Jene mechanische Saitenteilung tut jedoch dem Gehör ganz wohl Genüge... Wenn man aber das Urteil des Gehörs mit Verstand und Klugheit kritisch prüft, zeigt sich sofort ein Widerspruch. Ich will das folgendermaßen beweisen. Das Ohr anerkennt die Harmonie zwischen 100,000 und 50,363, wie der Praktiker behauptet. Die gleiche Harmonie anerkennt das Ohr aber auch zwischen 100,000 und 50,000, wie ich behaupte. Es fragt sich, ob das Ohr nichts von einer Verschiedenheit merkt und ob jener Harmonie eine solche Weise zukommt? Auf Grund meiner harmonischen Teilungen im 2. Kapitel antworte ich nein...."⁶

Er erklärt weiter, daß das Ohr genausowenig zwischen den Konsonanzen 100,000:50,000 und 100,000 zu 49,637 unterscheiden wird. Wenn man aber nun hinginge und die beiden Werte 50,363 und 49,637 nicht jeweils zusammen mit der ganzen Seite 100,000 anschlüge, sondern beide Teile nebeneinander, also 49,637 nach 50,363 anschlüge, so würde das Ohr sehr wohl den höheren Ton vom niedrigeren unterscheiden.

"Es ist also klar, daß das Ohr die Aussage, die Konsonanz zwischen 50,363 und 100,000 sei die gleiche wie die zwischen 49,637 und 100,000, nur macht, insofern 50,363 und 49,637 gleich zu sein scheinen, d.h insofern beide Konsonanzen sich nur unmerklich von der von 50,000 und 100,000 unterscheiden. Wenn daher das Ohr den Fragen des Verstandes entsprechend antwortet, wird es sagen, die genaue Harmonie bestehe zwischen 100,000 und 50,000..."⁷

An Keplers Zahlenbeispiel kann man hier die nach seiner Theorie berechneten Verhältnisse gut nachprüfen. Auch sieht man, daß, wenn man jetzt nach dem Prinzip stimmte und die Aufgabe hätte, in einer Tonleiter möglichst viele reine Intervalle zu erzeugen, so sähe man, daß man bereits bei der Bildung der Quinte auf dem zweiten Ton (a = 88,889) Schwierigkeiten bekäme, denn das Verhältnis zum e (60,000) ist nicht genau 3:2. Die reine Quinte würde durch 90,000:60,000 erfüllt. Andererseits muß man bedenken, daß die Charakteristik einer Tonart durch ihre eigenen vollkommenen Intervalle bestimmt wird, denn deren Konsonanz legt alle anderen Intervalle fest. Ein bemerkenswertes Charakteristikum ist der Unterschied zwischen kleinen und großen Halbtönen, der bei diesem Aufbau in jedem Falle entsteht!

Kepler greift auch eine andere Stimmung an, die Vincenzo Galilei sich ausgedacht hatte. Dabei macht er seine Haltung noch einmal ganz deutlich: Er billigt zwar das außerordentliche Geschick von Galileis mechanischem Verfahren, "das es möglich macht, bei der Verwendung der Instrumente fast die gleichen Nuancierungen zu erzielen wie mit der menschlichen Stimme". Doch er betont immer wieder, daß dies nicht die Lösung sein kann, denn die wahre Schönheit liegt in den Grundlagen der Geometrie, welche man nicht durchweg "mechanisch ausgleichen" dürfe:

"Für die Theorie aber, für die Erkenntnis des Wesens der Musik halte ich sein Vorgehen für verderblich; auch wird dabei das Instrument die freie Beweglichkeit der menschlichen Stimme doch niemals wirklich erreichen."⁸

Die Diskussion um die richtige Stimmung geht, wie wir wissen, bis auf den heutigen Tag weiter. Nach Kepler gab es viele gute Lösungsvorschläge, und es ist nicht erstaunlich, daß sich der große Musiktheoretiker, Komponist und Organist Andreas Werckmeister (1645-1706), der für Dietrich Buxtehude arbeitete und den Johann Sebastian Bach bei diesem kennenlernte, in seinen Werken - z.B. dem bereits 1686 in Frankfurt/Main und Leipzig erschienenen Buch Musicalische Temperatur, oder Deutlicher und warer mathematischer Unterricht, wie man durch Anweisung des Monochordi ein Clavier, sonderlich die Orgel-Wercke, Positive, Regale, Spinetten und dergleichen wol temperirt stimmen könne, ausdrücklich auf Johannes Kepler und seine Idee der "Harmonia Mundi" beruft.

Begeistert von seinen Ideen komponierte Bach sein "Wohltemperiertes Klavier". Gerade zu Bachs Zeiten tobte der Kampf zwischen den "Ausgleichern" mit ihrer "gleichschwebenden" Stimmung und den Kreisen um Johann Sebastian Bach, der auch selber Mathematiker sowie Orgelbauer war, auf das stärkste. Das "Wohltemperierte Klavier" ist der Beweis dafür, daß Bach auf keinen Fall in der "Gleichschwebung" temperiert hat. Wäre das der Fall, wie einige behaupten, hätte ein Präludium und eine Fuge, z.B. in cis-moll, gereicht. Bach liebte die Chromatik, die Herausarbeitung aller Tonleitercharaktere. Sein Standpunkt war, wie es Nikolaus Forkel beschreibt:

"Selbst der in der Mathematik so gelehrte Johann Sebastian Bach habe sich in diesen Fragen nach der Natur, nicht nach der Regel gerichtet, und die ganze Mathematisiererei habe noch nicht einmal den Erfolg gehabt, die Durchführung einer einwandfreien Temperatur zu gewährleisten."⁹

Deshalb ist das Klavierstimmen bis auf den heutigen Tag ein eigener Beruf oder, besser gesagt, eine wahre Kunst. Die wenigsten großen Pianisten stimmen alle Töne "gleichschwebend". Die Wahrheit liegt eben in der Geometrie oder der Physik selbst, von der die Mathematik immer nur ein "Mittel zum Zweck" bleiben wird. Denn wie Kepler schon erkannte:

"Groß ist das Vertrauen und die Zuversicht des Geistes, wo immer eine Ordnung zutage tritt. Die Ursache hierfür ist in den tiefsten ursprüngen der Geometrie zu suchen. Wenn auch einmal eine Ordnung durch Zufall bewirkt würde, so fliegen doch daselbst die Geister zusammen; darin liegt ihr Ergötzen, ihr Leben."¹⁰

Anmerkungen

1 - Johannes Kepler, Weltharmonik, III. Buch, S. 120 ff.
2 - Ebenda, S. 123 f.
3 - Ebenda, S. 124.
4 - Ebenda, S. 134.
5 - Ebenda, S. 135.
6 - Ebenda, S. 135 f.
7 - Ebenda, S. 136.
8 - Ebenda, S. 136.
9 - Heinrich Edelhoff, Johann Nikolaus Forkel, Göttingen, 1935, S. 240.
10 - Kepler, a.a.O., S. 5.