Noch zu Lebzeiten des Pythagoras wurden er und seine Anhänger durch eine Verleumdungskampagne aus Süditalien verjagt und nach dem Abbrennen ihres Versammlungshauses in Kroton in alle Winde zerstreut. Viele flohen nach Griechenland zurück, einige hielten sich noch länger in Italien auf, darunter vor allem Archytas von Tarent, der alle Erzählungen der Pythagoräer sammelte und in Büchern niederschrieb. Deshalb gilt er heute neben Historikern wie Nikomachus von Gerasa, Timaios der Geschichtsschreiber und natürlich Platon als eine der wichtigsten Quellen über die Pythagoräer. Wegen seiner Fähigkeiten war er lange Jahre hindurch Stratege von Tarent und arbeitete auf der Grundlage des Pythagoras weiter an den Ideen, vor allem in der Geometrie und Musik, doch den vielen in Griechenland zerstreuten Pythagoräern ging es ziemlich schlecht.
Es war zur Zeit des Peloponnesischen Krieges, als es mit der Moral Athens abwärts ging. In diese Zeit fallen auch die sogenannten "Komödien", und es traten überall Komödianten auf, welche die Ideen und Lehren des Pythagoras verleumdeten und lächerlich machten und seine verbliebenen Anhänger verhöhnten. Euripides (ca. 480-406 v.Chr.), einer der großen Dramatiker jener Zeit, der in seinen Werken die Dekadenz, Müßigkeit, Genußsucht und den Dionysuskult angriff, ging später - wie vor ihm schon die Dichter Sophokles (ca. 497/6-407/6 v.Chr.) und Aischylos (525-456 v.Chr.) - ins Exil.
In dieser Zeit vom Niedergang bis zum Untergang Athens verkam auch die Musik zum reinen Genußmittel, zur Untermalung kultischer oder kriegerischer Handlungen oder einfach zum Rauschmittel in der Ekstase (Ekstase = griechisches Wort für "Aussteigen"). Der Mensch galt als eine Kreatur des Zufalls. Friedrich Nietzsche ließ den Dionysoskult im 19. Jh. wieder aufleben und zitiert Silen, dessen Begleiter, der auf die Frage "Was ist das Allerbeste?" seinen Haß auf den Menschen als in der Geschichte stehendes Ideenwesen ausdrückt:
"Elendes Eintagsgeschlecht, des Zufalls Kinder und der Mühsal, was zwingst du mich, dir zu sagen, was nicht zu hören für dich das Ersprießlichste ist?
Das Allerbeste ist für dich gänzlich unerreichbar: nicht geboren zu sein, nicht zu sein, nichts zu sein. Das Zweitbeste aber ist für dich - bald zu sterben."
Erst 800 Jahre nach den griechischen Komödianten setzt Aurelius Augustinus (354-430 n.Chr.) aus Thagaste in Numidien, ein großer Verehrer Platons, in seinen Schriften, die er Platons Beispiel folgend in Dialogform verfaßt, ein Zeichen gegen den kulturellen Zerfall in der Zeit des untergehenden Römischen Reiches. Der Musiker und der Hörer müssen über das bloße Registrieren musikalischer Eindrücke und über die oberflächliche und sentimentale Hingabe an das Klangliche hinauswachsen, denn, so Augustinus, "die Seele will sich nicht vergeuden". Die Schönheit der Musik ist nicht nur im Wohlklang der einzelnen Töne begründet! Die wahre Schönheit hat eine viel tiefere Ursache. Diesem Hauptthema widmet er sein Werk über die Musik, De Musica, und erklärt im Dialog:
"Lehrer: Antworte mir also, ob du meinst, daß die Nachtigall richtig melodisch singt: ihr Gesang ist nämlich in den Intervallen geordnet, außerdem ist er sehr süß, und, wenn ich nicht irre, ist er auch der Jahreszeit entsprechend.
Schüler: Das alles scheint mir auch so.
Lehrer: Ist sie nun der freien Kunst fähig?
Schüler:
Nein...
Lehrer: Was hältst du nun von all denen, die wie jene Nachtigall, von irgendeinem Gefühl geleitet, richtig singen, das heißt mit der gehörigen Abmessung und mit schönem Ton; die aber, wenn man sie nach ihren eigenen Melodien und Intervallen, nach der Höhe und Tiefe ihrer Töne fragt, keine Antwort geben können?
Schüler: Ich glaube, sie sind der Nachtigall sehr ähnlich.
Lehrer: Und jene, die kenntnislos sich das gerne anhören, zum Beispiel Elefanten, Wölfe und andere wilde Tiere, die sich nach dem Klang der Musik bewegen... sind sie nicht alle miteinander vergleichbar?
Schüler: Ich glaube ja; aber leider finde ich fast bei allen Menschengattungen die gleiche Auffassung."1
Merkwürdig genug ist es, daß nach dem Zusammenbruch des Römischen Reichs im 4./5. Jh. n.Chr. eine solche Zerstörung in der Musik erfolgte, daß nicht nur die Tonleiterbenennungen der Pythagoräer vertauscht wurden (wie schon im Teil II beschrieben), sondern sogar das Wissen über den Aufbau der achtstufigen Tonleiter (und damit natürlich auch jegliches Wissen über deren geometrische Grundlage!) verloren ging. Papst Gregor I. (590-604 n.Chr.) spielt hier eine zerstörerische Rolle, denn durch seinen Einfluß setzt sich die - größtenteils pentatonisch, d.h. auf fünfstufiger Tonleiter basierende - nach ihm benannte "gregorianische" Musik durch. Diese "Musik" zeichnet sich durch eintöniges und einförmiges Geleiere aus, welches mit der naturgemäßen, die Gesetze des Universums widerspiegelnden Musik nichts mehr zu tun hat.
Erst zu Beginn des 15. Jh. mit der Renaissance, als vor allem auf Anregung Petrarcas und seines Freundes Boccaccio alte Schriften wiederentdeckt und übersetzt wurden, vollzieht sich auch die Wende von der Einstimmigkeit bzw. Eintönigkeit der Gregorianik zur Mehrstimmigkeit der Renaissance. Vergleichbar mit den Revolutionen in Architektur, Malerei und Städtebau, und den Ideen und Studien Luca Paciolis und Leonardo da Vincis, zeigte auch die Musik eines Guillaume Dufay (geb. um 1400, Hennegau), Johannes Ockeghem (um 1425, Flandern), Josquin de Prés (um 1450, Picardie), Heinrich Isaak (um 1450 Flandern) und Palestrina (um 1525, Rom), daß die geometrischen Grundlagen und die Erkenntnisse der Alten eine neue Idee der Mehrstimmigkeit erzeugt hatten.
Sie beruhte auf der von Pythagoras entdeckten Tatsache, daß der Mensch eine bestimmte ausgewählte Zahl von Proportionen als "synphon" hört. Diese Tatsache, welche alle anderen Proportionen zu Dissonanzen macht2, und dadurch bedingt, daß der mehrstimmigen Komposition bestimmte Gesetzmäßigkeiten zugrundeliegen müssen, wirft die Frage auf: Was macht die Musik "schön"? Gibt es Gründe dafür, daß der Mensch nur bestimmte Intervalle als "Konsonanzen" hört? Welche Gründe sind es, die bestimmte Musik "eintönig" werden, andere aber eine unaussprechliche Schönheit ausdrücken lassen, die nicht in Worte zu fassen ist?
Kepler mischte sich in die Diskussionen der Musiktheoretiker und Komponisten seiner Zeit ein, und es muß zu teilweise erbitterten Gefechten zwischen den Anhängern von Vincenzo Galilei (1520 oder 1533-1591), Michael Praetorius (um 1572-1621), Glarean (1488-1563) und Giovanni Maria Artusi (1540-1613) gekommen sein.3
Die entscheidenden Fragen reichten tief in die Grundlagen der Musik, die Vorstellung vom Universum und vor allem die Rolle des Menschen in ihm. Der Hauptstreitpunkt war: Wie soll man Instrumente stimmen? Denn bei Instrumenten mit festgelegten Tönen, wie der Laute oder der Orgel, steht man vor dem schon im I. Teil angesprochenen Paradox, daß einerseits das menschliche Ohr nur ganz bestimmte Intervalle als "schön" und "harmonisch" hört, andererseits dadurch in jeder einzelnen Tonleiter die Tonabstände minimal verschieden sind. Diese notwendige Flexibilität der einzelnen Töne ist auf Instrumenten schwer zu erreichen. Eine gut ausgebildete menschliche Singstimme singt dagegen jede Tonart "richtig".
Dieses Paradox ergibt sich aus der einfachen Tatsache, daß die "synphonen" oder "konsonanten" Intervalle durch ganzzahlige Unterteilungen einer Saite erzeugt werden. Rein aus der mathematischen Charakteristik der rationalen Zahlen kann man in einer Zahl von Tönen untereinander immer wieder ganzzahlige Verhältnisse bilden. Wenn Sie acht Zahlen aufschreiben, die untereinander möglichst viele ganzzahlige Verhältnisse aufweisen (sagen wir 1:2, 2:3, 3:4, 4:5 und 5:6, d.h. die Intervalle der Konsonanzen, die der Mensch als schön empfindet), so wären die kleinsten Zahlen, bei denen das möglich ist, die Zahlen 24, 27, 30, 32, 36, 40, 45 und 48.
Sie können das leicht nachprüfen: Zwischen 24 und 48 besteht das Verhältnis 1:2, zwischen 24 und 30 das Verhältnis 4:5, zwischen 24 und 36 das Verhältnis 2:3 und so weiter. Wenn Sie aber auf der 27 das Verhältnis 2:3 erzeugen wollen, so finden sie keine passende ganze Zahl in dieser Reihe.
Musikalisch gesprochen heißt das: wenn man auf der zweiten Stufe die Quinte (Verhältnis 2:3) aufbauen will, welche eigentlich fünf Töne weiter bei 40 liegen sollte, so stellt sich die 40 als zu klein heraus, um eine reine Quinte zu erzeugen. Die reine Quinte liegt ein ganz klein wenig höher, bei 40,5. Sagen wir, die 24 sei das c einer Tonleiter, die 27 das d, 30 das e usw., dann wäre dieses a (die 40) zu niedrig für eine Tonleiter, die auf dem d (der 27) begänne.
Und hierin besteht das Paradox, um das es hier geht. Es bewirkt, daß jede Tonleiter eine eigene Charakteristik oder Farbe (= chroma) besitzt. Der Streit ging nun darum, ob man die Tonhöhen alle untereinander angleichen sollte, so daß die konsonanten Intervalle zwar von ihrer Harmonie verlören, dafür aber solche Schwierigkeiten, welche die ständige notwendige Veränderung der einzelnen Töne mit sich brachte, vermieden werden könnten (was man auf den Instrumenten der damaligen Zeit, wie z.B. den Orgeln, sowieso nicht machen konnte; so flexibel ist nur die menschliche Stimme oder die erst im 16. Jh. entwickelten Instrumente der Geigenfamilie - Violine, Viola, Cello und Kontrabaß).
Die eine Partei, der auch der berühmte Mathematiker Vincenzo Galilei und später seine Anhänger angehörten, sagte, die Mathematik sei die Königin, man könne durchaus durch geschickte Rechnerei mit den kleinsten Kompromissen eine Angleichung schaffen. Die andere Partei verteidigte vehement die von der Natur geschaffene höhere Geometrie, die schließlich durch die ganz besondere Färbung der Tonleitern zutage trete und die eigentliche Schönheit der Musik ausmache.
Wer kann das entscheiden? Nimmt man an, daß die Schönheit und alle großen Empfindungen, welche die Musik in der Seele auszulösen vermag, rein "sinnliche" Eindrücke sind - dann erscheint Galileis Argument richtig, denn mit einer guten mathematischen Berechnung und Angleichung der Intervalle, so daß sie in allen Tonleitern "passen", richtet man alles ein bißchen gerade, "korrigiert" sozusagen die ganzzahligen Verhältnisse - vom Ohr kaum hörbar - ein wenig nach oben oder unten, und vermeidet zu große Spannungen.
In diesen Streit mischt sich nun der Astronom Johannes Kepler ein und beweist dabei sein unglaubliches musikalisches Verständnis. Das tut er in ziemlich "pythagoräischer" Weise. Er beginnt eine Untersuchung der geometrischen Gesetzmäßigkeiten und der Harmonie des Universums:
"Denn bitte, welche Beziehung soll bestehen zwischen der Reizung des Gehörs, eines körperlichen Dings, und dem unglaublichen Lustgefühl, das wir über die harmonischen Konsonanzen ganz tief in unserem Innern empfinden? Wenn überhaupt das Lustgefühl von der Reizung herrührt, spielt dann nicht bei diesem Lustgefühl das Organ die Hauptrolle, das die Reizung aufnimmt? In der Dioptrik bin ich darauf gekommen, jeden Sinn so zu definieren, daß die Lust oder Schmerz erzeugende sinnliche Wahrnehmung dann erst abgeschlossen ist, wenn die Spezies des dieser Wahrnehmung dienenden Organs, sobald dieses von außen her affiziert worden ist, einwärts durch das Geleit der Lebensgeister vor das Tribunal des allgemeinen Sinnes gelangt. Nun aber frage ich, welchen Anteil an der Lust haben beim Hören konsonanter Stimmen und Töne die Ohren?... Dazu kommt noch ein Weiteres. Die von der Bewegung hergeleitete Erklärung bezieht sich nicht in erster Linie auf den Einklang, sondern auf die anderen Konsonanzen und ihre Zusammensetzung..."4
Kepler kommt zu dem Schluß, daß es die Instanz der Seele, der geistigen Erkenntnis ist, welche mit der Schönheit der Gesetze verknüpft ist und diese letztendlich erkennt:
"Die Verrichtungen und Bewegungen der Körper, in denen die harmonischen Proportionen nachgeahmt werden, sprechen für Seele und Geist, indem sie diesen die Ursache bezeichnen, warum die Konsonanzen Ergötzen hervorrufen. Auch das Urteil der Alten steht damit nicht in Widerspruch. Wenn sie die Seele bald als Bewegung, bald als Harmonie definieren, so haben sie nicht so fast ungereimtes Zeug gesprochen, sie sind vielmehr nicht richtig verstanden worden, da sich häufig in schwierigen Fragen unter der Hülle des Worts ein mystischer Sinn verbirgt. Die Philosophie des Timäus aus Lokri, nach der die Seele aus harmonischen Proportionen zusammengesetzt ist (wovon in der Einleitung die Rede war), wurde von Aristoteles in dem Sinn widerlegt, den der Wortlaut ausdrückt. Ich möchte aber keineswegs behaupten, daß in jenen Zeilen nur das steckt, was der Wortlaut besagt. Ja, ich glaube, niemand wird bestreiten, daß jener Autor zum mindesten in dem Grundgedanken, den ich aufstelle, festhält, daß es nämlich des Menschen Seele und Geist ist, durch deren Urteil oder Instinkt der Gehörsinn die angenehmen, d.h. konsonanten Proportionen von den unangenehmen oder dissonanten unterscheidet. Legt er doch sorgfältig Bedacht auf die Erwägung, daß die Proportionen Verstandesdinge sind und nur durch den Verstand, nicht durch die Sinne erfaßt werden können, und daß es eine Funktion des Geistes ist, die Proportionen, d.i. die Form von dem proportionierten Ding, d.i. die Materie, zu unterscheiden."5
Johannes Kepler macht sich seine eigenen Gedanken über die Ursache der Harmonie. Er sucht den Grund in den ebenen, natürlich regelmäßigen Figuren, den Kreisteilungen. Darin sieht er den Grund für die "Konsonanz", weil diese Figuren mit den Qualitäten der Dinge in Verbindung stehen, während die räumlichen Gebilde ein Analogon zu den Substanzen sind. Er nennt sie die "weltbildenden Verhältnisse". Doch was zeichnet diese in der Geometrie vor allen anderen so sehr aus, daß die Seele nur sie allein als "schön" akzeptiert? Denn es sind ja allein die durch die Geometrie dargebotenen Zahlen und Größen, die der Mensch richtig erfassen kann.
Warum sind aus den unendlich vielen regelmäßigen Figuren (den Vielecken des Kreises) genau diese sieben konsonanten Verhältnisse - 1:2, 2:3, 3:4, 4:5, 3:5, 5:6 und 5:8 - etwas "Besonderes"? Sind es genau die regulären Vielecke, welche man mit Zirkel und Lineal konstruieren kann? Also das Dreieck, Viereck, Fünfeck, Sechseck, Achteck, Zehneck, Zwölfeck, Sechzehneck, Zwanzigeck und so weiter...? Das sind immer noch viel zu viele. Wenn aber all die ausgeschlossen wären, die durch reine Teilungsprozesse aus vorherigen entstehen? Dann wäre das Achteck ausgeschlossen. Das konsonante Verhältnis 5:8 entsteht aber offensichtlich aus dem Achteck.
Und wenn all diejenigen ausgeschlossen werden, die nicht mit Hilfe anderer Vielecke konstruiert werden können, so daß das Fünfzehneck z.B. wegfällt? Wir sehen schon, welche Überlegung Kepler antreibt, genau die obigen sieben Verhältnisse herauszufiltern. Seinem eigenen Zeugnis nach probierte er Tausende verschiedene Formen und Wege, um dieser Frage Herr zu werden. Aber erst in seinem Spätwerk Harmonia Mundi (Weltharmonik) gelangt er zu der Lösung:
"Aus diesen Gründen habe ich seit zwanzig Jahren das Ziel meines Strebens darin erblickt, diesen Teil der Mathematik und Physik klarer zu begründen. Ich wollte Ursachen ausfindig machen, die einerseits bei der Zahl konsonanter und melodischer Intervalle das Urteil des Gehörs befriedigen und über das, was das Ohr erfordert, nicht hinausgehen, die andererseits einen klaren und offensichtlichen Unterschied erkennen lassen zwischen den Zahlen, die musikalische Intervalle bilden, und denen, die hiezu untauglich sind, und die schließlich im Hinblick sowohl auf das Urbild wie auf den Geist, der sich des Urbildes bedient, um die Dinge ihm entsprechend zu gestalten, eine Verwandtschaft mit den Intervallen haben und daher auf größter Wahrscheinlichkeit beruhen... Und da es ein Geisteswesen ist, das die menschlichen Seelen so gebildet hat, daß sie sich an einem solchen Intervall ergötzen (darin liegt die wahre Definition der Konsonanz), müssen auch die Unterschiede des einen Intervalls vom anderen sowie die Ursachen, warum diese Intervalle harmonisch sind, geistiger und intelligibler Natur sein..."6
Keplers Idee beruht darauf, daß er die schwingenden Saiten der Instrumente oder die Längen der Stimmbänder des Menschen eigentlich als auseinandergezogene Kreise betrachtete, und daß durch Anklingen oder Singen der konsonanten Intervalle eine Teilung dieser Kreise in reguläre Vielecke bewirkt wird. Wie soll man sich das vorstellen?
Denken wir einmal an das Experiment des Pythagoras am Monochord. War es nicht tatsächlich so, daß der eine Teil der Saiten ebenfalls in aufgeteilten Bögen mitschwang, je nachdem, den wievielten Teil der ganzen Saite man abgeteilt hatte?
Kepler fand nach langen Überlegungen die Forderungen, welche die Kreisteilungen erfüllen müssen, damit das durch sie erzeugte Intervall vom Ohr als konsonant gehört wird. Diese sind:
1) Alle Kreisteilungen müssen allein mit Zirkel und Lineal erzeugt werden können, also "konstruierbare und reguläre Figuren" sein.
2) Dabei müssen sie auch "eigentliche" Kreisteilungen sein, d.h. ohne die Hilfe anderer Vielecke konstruierbar sein.
3) Die Kreisteilungen müssen "weltbildende Verhältnisse" sein, d.h. selber wieder ausschließlich konsonante Verhältnisse erzeugen, (das bedeutet, daß die beiden bei der Teilung entstehenden Kreisteile sowohl unter sich als auch jeweils mit dem ganzen Kreis wieder nur Verhältnisse bilden dürfen, die ebenfalls zu einer "konstruierbaren regulären" Figur gehören sowie eine "eigene" Konstruktion besitzen).
|
|
Diese Forderungen aber erfüllen nur die folgenden Verhältnisse: 2:3 (erzeugt durch das Dreieck), 3:4 (erzeugt durch das Viereck), die Verhältnisse 4:5 und 3:5 (aus dem Fünfeck), 5:6 (aus dem Sechseck) sowie das Verhältnis 5:8 (erzeugt aus dem Achteck). Betrachten wir nun diese "weltbildenden Verhältnisse" genauer:
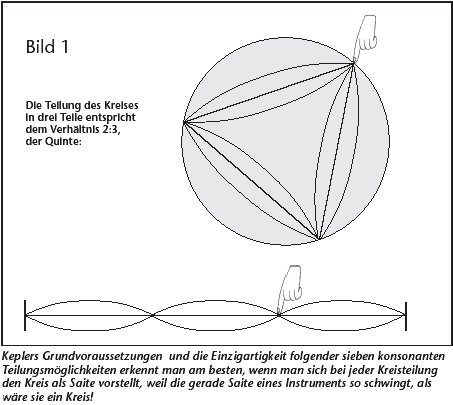
Die Quinte, das nach Pythagoras Experiment nachgewiesene Verhältnis 2:3, entsteht durch Dreiteilung des Kreises; sie entsteht durch ein Dreieck (siehe Abb. 1), bei dem eine Ecke festgehalten wird.
Keplers Grundbedingungen und die Einzigartigkeit dieser sieben konsonanten Teilungsmöglichkeiten sieht man am besten, wenn man sich bei jeder Kreisteilung den Kreis als Saite vorstellt, weil die gerade Saite eines Instruments so schwingt, als wäre sie ein Kreis!
Durch Zupfen des längeren Teils der Saite ertönt die Quinte 2:3 zum Grundton, durch Zupfen des kürzeren Teils die Oktave 1:2 dieser Quint, d.h. die Duodezime des Grundtons. (Zu bemerken ist, daß es beim Dreieck egal ist, welche Ecke festgehalten wird, denn es entsteht jedes Mal dasselbe Verhältnis. Daher zeichnet sich die Quinte besonders aus.)
Die Quarte, nach Pythagoras 3:4, wird durch die Vierteilung des Kreises erzeugt; sie entsteht durch das Viereck, bei dem ein Teil festgehalten wird (siehe Abb. 2).
Zupft man den längeren Teil der Saite an, ertönt die Quarte 3:4 zum Grundton, zupft man aber an dem kürzeren Teil (1:3), so ertönt die Quinte zur Quarte, also die Oktave des Grundtons.
(Hielte man beim Viereck zwei Teile fest, so bekäme man die Teilung 2:4, welches wieder das doppelte Verhältnis des Grundtons, die Oktave wäre. Daher zeichnet sich auch die Quarte besonders aus, und Kepler nennt diese beiden Konsonanzen - Quarte und Quinte - die vollkommensten.)
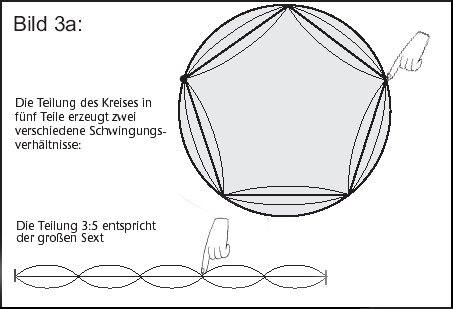
Aus dem Fünfeck entstehen nun zwei konsonante Intervalle, die große Sexte 3:5 und die große Terz 4:5. Sie entstehen dadurch, daß beim Fünfeck einmal der dritte, einmal der vierte Teil festgehalten wird (siehe Abb. 3 a und b):
Bei der Teilung 3:5 ertönt beim Zupfen des längeren Teils die große Sexte zum Grundton; wenn man aber den kürzeren Teil anzupft (siehe Abb. 3 a), ertönt die Quinte zu dieser großen Sexte (weil die kürzere zur längeren Saite im Verhältnis 2:3 steht).
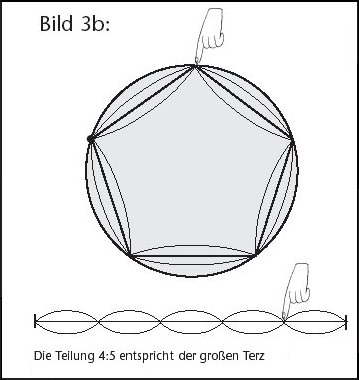Bei der Teilung 4:5 entsteht die große Terz, die man hört, wenn man den längeren Teil 4 zur Grundsaite 5 zupft; zupft man aber an dem kurzen Teil (siehe Abb. 3 b), erklingt die Oktave zur großen Terz.
Das Sechseck (siehe Abb. 4) erzeugt ein einziges neues konsonantes Intervall, die kleine Terz 5:6, indem ein Teil von sechsen festgehalten wird:
Zupft man hierbei am längeren Teil der Saite, so erklingt die kleine Terz 5:6 im Verhältnis zum Grundton; zupft man aber an dem kurzen Teil, so erklingt die Duodezime der kleinen Terz, ihre oktavierte Quinte. (Andere Teilungen des Sechsecks wie 2:4 oder 3:6 würden nur wieder die doppelte Schwingung des Grundtons ergeben.)
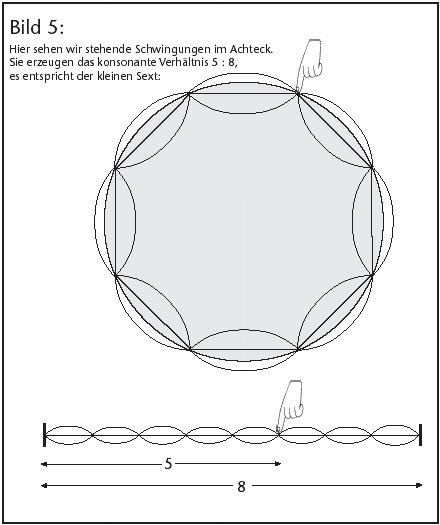
Die kleine Sexte wird noch durch die einzige beim Achteck erlaubte Teilung 5:8 erzeugt (siehe Abb. 5), indem vom Achteck fünf Teile festgehalten werden:
Zupft man hier an dem längeren Stück der Saite, so klingt also die kleine Sexte zur Grundsaite; wenn man aber an dem kürzeren Stück zupft, erhält man die große Sexte zu dieser kleinen Sexte.
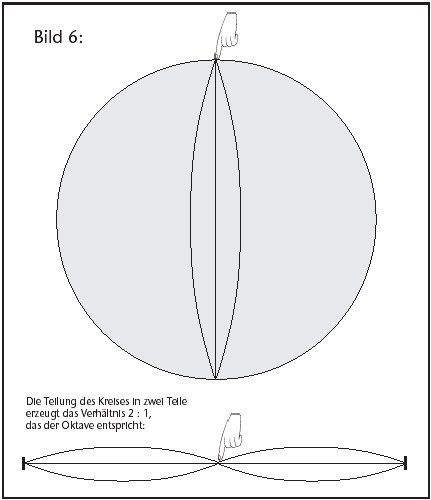
Die harmonischste Proportion aber haben wir noch vergessen: das Verhältnis 1:2, die Teilung in genau die Hälfte der Saite, bzw. den Halbkreis (siehe Abb. 6)! Der Durchmesser erzeugt die Oktave.
Kepler, begeistert über seine Entdeckung dieser wunderbaren Zusammenhänge, beschreibt den Grund, warum dieses Intervall als das vornehmste vor allen anderen so harmonisch mit dem Grundton vereint klingt:
"Die Konsonanz der Hälfte mit dem Ganzen ist nach dem Einklang die einzige vom ersten Grad, sie ist einfach, vollkommen und identisch, und zwar entgegengesetzt identisch...
Denn 1. Alle Seiten oder Figuren stehen in gleicher Weise vom Mittelpunkt ab; der Durchmesser geht durch ihn hindurch. 2. Teilt man den Kreis von einem Punkt aus mit der Seite einer Figur als Meßstrecke, so wird man, wenn man dies soundso oft gemacht hat, schließlich mit dem zweiten Endpunkt der Seite zu dem Ausgangspunkt zurückkehren; der Durchmesser aber, der durch den Mittelpunkt hindurchgeht, kehrt sogleich nach der ersten Wiederholung zum Anfangspunkt zurück... 7. Schließlich teilen die übrigen Figuren den Umfang des Kreises in soundso viele gleiche Teile, den Inhalt des Kreises aber in ungleiche Teile; denn in der Mitte bleibt ein Flächenstück, d.h. der Inhalt der Figur, übrig, das größer ist als einer der Kreisabschnitte. Der Durchmesser teilt nicht nur den Umfang, sondern auch den Inhalt in zwei gleiche Teile...
So liefert uns also der Durchmesser die wahre Ursache dafür, daß der Ton der ganzen Seite und der Ton der halben, obwohl verschieden, vom Gehör doch in gewisser Weise für gleich gehalten werden, im Vergleich zu den übrigen Konsonanzen. Es ist vergeblich, wenn andere die Ursache für diesen Gleichklang in der Zahl der 8 Töne suchen, da der Gleichklang von Natur aus früher ist als die Teilung dieses Intervalls in die 7 melodischen Intervalle, durch welche die 8 Töne bestimmt werden."7
Mehr als diese sieben Konsonanzen, die die Forderungen Keplers
erfüllen, kann es tatsächlich nicht geben. Das kann man selber nachprüfen: Sieben- und Neuneck fallen weg, weil sie nicht mit Zirkel und Lineal konstruierbar8 sind, das Zehneck, weil es aus Teilungen des Fünfecks entsteht, also keine eigene Konstruktion hat, aber auch, weil die Teilung des Zehnecks nur Verhältnisse liefert, die bereits da sind, wie 4:6 (das wäre das gleiche wie 2:3) oder 5:5 (das wäre natürlich wieder die Oktave, weil dabei die Saite genau in zwei Teile geteilt wird), das Fünfzehneck, weil es nicht aus einer "eigentlichen" Teilung entsteht, d.h. nicht konstruierbar ist ohne die Dreiteilung des Winkels, usw..
Tatsächlich gibt es entsprechende Experimente des Physikers Ernst F. Chladni, dem Lehrer der Brüder Ernst, Heinrich und Wilhelm Weber. Er bestreute Glasplatten mit Sand. Wenn er diese Platten dann an der Seite mit einem Geigenbogen anstrich, so daß sie in Schwingung gerieten, bildeten sich im Sand geometrische Formen, indem der Sand nur an bestimmten, wohlgeordneten Linien hochsprang, sonst aber unbewegt auf der Platte liegenblieb. Die auf diese Weise entstandenen Formen sind regelmäßige Vielecke - als hätte der jeweils erzeugte Ton einen Kreis zum Schwingen gebracht und diesen in bestimmte Teile geteilt!
Betrachten wir noch Keplers weitere Untersuchungen, wie er aus dem Vergleich der sieben Konsonanzen untereinander die Verhältnisse aller Töne einer Tonleiter erhält, die er melodische und Intervalle dritter Art nennt, kleine wie große Ganztonschritte. Außerdem erklärt er den geometrischen Grund dafür, daß die einzelnen Töne in jeder Tonart - die alle mit einem anderen Anfangston beginnen - verschiedene Frequenzen haben müssen, sowie den Unterschied zwischen Dur und Moll. Dies werden wir im vierten und letzten Teil der Serie kennenlernen.
Fortsetzung folgt
1 - Aurelius Augustinus, De Musica, Deutsche Augustinus-Ausgabe, 1962, S. 12.
2 - Diese Tatsache nutzt der später entwickelte Kontrapunkt dazu, die Konsonanzen durch Erzeugung und Auflösung von Dissonanzen zu verstärken.
3 - Praetorius verfaßte selber ein Manuskript zur Stimmung von Orgeln, Artusi verfaßte eine mehrfach aufgelegte Kontrapunktlehre und ist außerdem bekannt durch seine heftige Kritik an Claudio Monteverdis Kompositionsstil. Glarean (eigentlich Henricus Loriti, Glarean genannt wegen seiner Abstammung aus Glarus in der Schweiz) war ein enger Freund des Erasmus von Rotterdam und wird von einigen wegen seiner Kritik an der Tradition des Gregorianischen Chorals und seiner Begründung eines in sich stimmigen Tonleitersystems (anlehnend an das griechische) als "Retter der Musik aus dem Geist der Antike" bezeichnet.
4 - Johannes Kepler, Weltharmonik, III. Buch, S 100.
5 - Ebenda, S 100.
6 - Ebenda, S. 100 f.
7 - Ebenda, S.102 f.
8 - Das Neuneck vor allem, weil die Dreiteilung des Winkels unmöglich ist - das bewies zum ersten Mal Carl Friedrich Gauß.
Zurück zur Kultur-Hauptseite:
