April 2005:
Warum ist das Schöne schön? (Teil II)
Die Entdeckung der geometrischen Ursachen der musikalischen Harmonie von Pythagoras und Kepler
II. Teil: Vom Ursprung des Gesangs
Im zweiten Teil ihrer Serie über die geometrischen und
physikalischen Grundlagen des Schönen zeigt Caroline Hartmann, wie die
Pythagoräer ihr Tonsystem konstruierten.
Im ersten Teil des Artikels lernten wir die Entdeckung des Pythagoras kennen, die zeigt, daß die Saite eines Monochords (vereinfacht eine auf ein Stück hohles Holz gespannte Saite) - wenn man einen Teil von ihr mit dem Finger herunterdrückt, der zur ganzen Saite in einem ganzzahligen Verhältnis steht - in ebenso vielen Teilen schwingt. Physikalisch erklärten wir uns das mit dem Entstehen einer stehenden Welle mit genau dieser Anzahl von Teilen.
Doch das Phänomen, daß die Saite praktisch "weiß", der wievielte Teil der Saite vom Finger abgedrückt wurde, konnten wir uns nicht erklären. Es muß eine geometrische Eigenart der Natur und der Musik dahinterstecken. Und damit waren wir wieder bei der Anfangsfrage: Warum hat die Musik eine solch große Macht? Sie kann unser Innerstes aufwühlen, unsere Seele bewegen - warum? Es war uns bereits klargeworden, daß es nicht eine reine Gefühlssache sein kann, die das bewirkt. Doch bedeutet die Entdeckung des Pythagoras nun, daß die Musik rein geometrisch erklärbar ist, alle Empfindungen der Seele erklärbar durch schnöde Mathematik? Und wir fragten uns, ob diese geometrischen Vorgänge in der Natur etwa mit unserer Seele irgendwie zusammenhängen?
Die Frage, was die Seele eigentlich sei, hat die Menschen schon immer
beschäftigt, vielleicht noch nicht deutlich oder bewußt, aber doch in Ansätzen. Aber erst Pythagoras und die Pythagoräer, und als deren "Erbe" Platon, haben uns vermittelt, was andere lange vorher ahnten: die menschliche Seele ist unsterblich!
"Wir müssen also zuerst über die Natur der Seele, der göttlichen und der menschlichen, die richtige Einsicht gewinnen, indem wir ihre Leiden und Taten betrachten. Am Anfang des Beweises steht der Satz: Eine jede Seele ist unsterblich. Denn das aus sich selbst Bewegte ist unsterblich. Was aber anders bewegt wird, das zeigt in seiner Bewegung und auch in seinem Leben einen Unterbruch. Einzig das sich selbst Bewegende, weil es nämlich sich selbst nie verläßt, hört auch nie auf, bewegt zu werden, sondern wird auch für alles andere, was bewegt wird, Quelle und Ursprung der Bewegung... So ist also der Ursprung der Bewegung das sich selbst Bewegende, dies aber kann weder untergehen noch entstehen, sonst müßte alles, sowohl der Himmel als die ganze Schöpfung, zusammenfallen und stillestehen, und sie hätten nie wieder etwas durch das sie bewegt und zum Entstehen gebracht werden könnten. Nachdem sich also gezeigt hat, daß das von sich selbst Bewegte unsterblich ist, wird sich niemand zu sagen scheuen, daß eben dies das Wesen und der Begriff der Seele sei..."1
Auf welche Weise bewegt sich aber die Seele selbst? Ist es möglich, daß sie vor allen anderen schönen Künsten die Musik als ihre "Heimat", ihre innerste eigenste Bewegung erfährt? Wie entstand denn die Seele, wie entstand die Musik? Wenn man sich die tonalen Grundlagen der chinesischen, indischen oder islamischen Musik anschaut, so kann man den gemeinsamen Ursprung dieser Musik und der pythagoräischen erkennen.
Anders gesagt: Wie bei der Sprache, der Entwicklung der Poesie sowie der Musik findet man ein- und denselben Ursprung in den verschiedenen Kulturen. So wie es bekanntlich Märchen aus alten Überlieferungen gibt, die - obwohl sie in ganz verschiedenen Teilen der Welt entstanden - sich so verblüffend ähnlich sind, als hätte sie derselbe Poet verfaßt.
Genauso gibt es Beispiele über die gleichzeitige Entstehung von
Musikinstrumenten: die antike Lyra (oder Leier), welche zur Zeit des Pythagoras gespielt wurde, verschwand nach dem Untergang des römischen Weltreichs aus dem mitteleuropäischen Raum. Sie kommt im Mittelalter überhaupt nicht vor, und es hat auch keine mittelalterliche Leier die Züge der antiken Kithara. Doch gab es eine andere Leier, die als Begleitinstrument der keltischen Barden im 1. Jh. v.Chr. galt, doch ist es schwer zu sagen, woher die Kelten diese Leier hatten. Sie ähnelt der einzigen bis heute in Asien erhaltenen Leier der Ostjaken. In Deutschland tauchte eine solche, auffallend schmale Leier in einem
alemannischen Kriegergrab aus der Mitte des 1. Jh. n.Chr. auf.2
Wenn man nach einem "Ursprung" der Musik fragt, so kann man dem
Sprachforscher Jacob Grimm folgen, der bei der Untersuchung der Frage, ob die Sprache gleich bei der Schöpfung entstand oder etwa ein Geschenk Gottes an den Menschen nach der Schöpfung war, zu folgendem Schluß kam:
"Ich habe, worauf mein Ziel sich beschränkte, dargetan, daß die
Menschensprache so wenig eine unmittelbar geoffenbarte sein könne, als eine anerschaffne war; eine angeborne Sprache hätte die Menschen zu Tieren gemacht, eine geoffenbarte in ihnen Götter vorausgesetzt. Es bleibt nichts übrig, als daß sie eine menschliche, mit voller Freiheit ihrem Ursprung und Fortschritt nach von uns selbst erworbne sein müsse: nichts anders kann sie sein, sie ist unsre Geschichte, unsre Erbschaft.
Das was wir sind, wodurch wir uns von allen Tieren unterscheiden, führt im Sanskrit den bedeutsamen ehrwürdigen Namen manudscha... Der Mensch heißt nicht nur so, weil er denkt, sondern ist auch Mensch, weil er denkt, und spricht, weil er denkt, dieser engste Zusammenhang zwischen seinem Vermögen zu denken und zu reden bezeichnet und verbürgt uns seiner Sprache Grund und Ursprung... Das Kind beginnt zu reden, wie es anhebt zu denken, und die Rede wächst ihm, wie ihm der Gedanke wächst..."3
Die Sprache wurde ja von Anbeginn oft mit Musik untermalt, wenn es feierlich oder festlich und freudig zuging, das belegen viele Zeugnisse über den sogenannten "Sprechgesang". Daher kann man die Erklärung auch auf den Gesang und die menschliche Musik anwenden. Der Mensch erahnte und entdeckte dabei immer mehr die Gesetze des Klangraums. Bereits in den ältesten Instrumenten, die wir heute kennen, gibt es Ansätze vom Verständnis eines "geordneten" Aufbaus der Töne.
Kürzlich entdeckte man eine 37 000 Jahre alte Flöte aus Mammutelfenbein und eine Schwanenflügelknochenflöte, deren Alter man auf 35 000 Jahre schätzt. Sie bezeugen nicht nur eine hochgradige Kunstfertigkeit bei der Verarbeitung zerbrechlicher Materialien (vor allem Elfenbein) und die Tatsache, daß Musik im Leben unserer eiszeitlichen Vorfahren eine bedeutende Rolle spielte, sondern auch eine Idee.
Das Prinzip dieser Flöte mag uns heute einfach erscheinen, sie besteht ja nur aus einem kleinen Rohr aus Knochen bzw. Elfenbein, doch es steckt eine wichtige Erkenntnis dahinter. Man macht sich nämlich gar nicht klar, warum es eigentlich Löcher in diesem Rohr gibt, und warum gerade zwei? Hatte man vielleicht schon eine Idee davon, daß die durch Laute angeregte Luft schwingt, daß die Länge einer Luftsäule und ihre Unterbrechung etwas mit verschiedenen Tonhöhen zu tun hat? Das Prinzip des Intervalls, des Zusammenklangs zweier Töne, ohne welches das menschliche Ohr laut Leonardo da Vinci keine Töne als Musik identifiziert, müssen unsere Vorfahren also erkannt haben, wenn auch nicht eine genaue geometrische Aufteilung einer ganzen Reihe von Tönen bzw. der Tonleiter.
Ebenso findet man die Entdeckung, daß eine Luftsäule in einem länglichen Rohr schwingt, und daß durch das Anzupfen einer einzelnen Saite (also eines gespannten Seils, Fadens oder Haares) die Luft zum Schwingen gebracht wird. Diese Schwingung kann man ja sogar beobachten, und vielleicht war dies der Ausgangspunkt, sich eingehender mit diesen Zusammenklängen zu beschäftigen?
Seit den ersten Ideen über Luftschwingungen, Töne und Intervalle hat sich das musikalische Verständnis immer weiter entwickelt. Die Idee der Schönheit, die Freude an neuen Entdeckungen waren der Antrieb, daß die Möglichkeiten der musikalischen Praxis immer weiter fortschritten. Die Musik sollte mindestens so schön sein wie der Gesang der Vögel, doch bestimmter und bewußter dort, wo die Sprache nicht ausreichte, Gefühle und Bewegungen der Seele auszudrücken! Ja, die Musik war neben der Astronomie das Gebiet, wo der Mensch eine gewisse Ordnung erahnte, ohne sie noch ganz greifen zu können: die geometrische Ordnung der Planetenbahnen und die der Töne.
 Wie soll man einen Ton ganz genau beschreiben? Bei den ersten Lyren lagen die einzelnen Töne ziemlich weit voneinander entfernt (siehe Abb. 1), doch legte man sie mit der Zeit immer enger aneinander. Wenn Sie einmal
einen möglichst hohen Ton, dann einen möglichst tiefen und zum Schluß einen zwischen diesen beiden singen, und danach versuchen, den ersten hohen Ton wieder genau zu treffen, bekommen Sie eine Vorstellung, wie schwer es ist, sich den Klangraum so genau einzuteilen, daß es eine replizierbare Ordnung gibt. Einige Instrumentenbeispiele zeigen, daß es Hochkulturen gab, die eine sehr weitentwickelte Kenntnis vom wirklichen Aufbau des Klangraumes hatten, doch sind keine schriftlichen Erkenntnisse dieser Zeit überliefert.
Wie soll man einen Ton ganz genau beschreiben? Bei den ersten Lyren lagen die einzelnen Töne ziemlich weit voneinander entfernt (siehe Abb. 1), doch legte man sie mit der Zeit immer enger aneinander. Wenn Sie einmal
einen möglichst hohen Ton, dann einen möglichst tiefen und zum Schluß einen zwischen diesen beiden singen, und danach versuchen, den ersten hohen Ton wieder genau zu treffen, bekommen Sie eine Vorstellung, wie schwer es ist, sich den Klangraum so genau einzuteilen, daß es eine replizierbare Ordnung gibt. Einige Instrumentenbeispiele zeigen, daß es Hochkulturen gab, die eine sehr weitentwickelte Kenntnis vom wirklichen Aufbau des Klangraumes hatten, doch sind keine schriftlichen Erkenntnisse dieser Zeit überliefert.
Erst Pythagoras demonstrierte am Beispiel des Monochords, daß der Klangraum nicht willkürlich, sondern sehr "geometrisch geordnet" aufgebaut ist. Ebenso war Pythagoras der erste, der nach der Ursache dafür fragte, warum die menschliche Seele nur ganz bestimmte ausgewählte Intervalle als harmonisch und schön, als "synphon" erkennt. Also hat Schönheit doch mit Geometrie zu tun? Und was hat die Seele damit zu tun?
Betrachten wir noch einmal die Unterteilungen der Saite des Monochords, womit Pythagoras die "synphonen" Intervalle demonstriert hatte. Die als "synphon" ausgezeichneten Intervalle waren 2:1, 3:2, 4:3 und bei Archytas noch 5:4. Nun fand Pythagoras folgendes heraus: Das beobachtete Schwingungsphänomen, d.h. die Unterteilung der längeren Enden der mit dem Finger heruntergedrückten Saite - wie mit "Geisterhand" - zeigt, daß durch die Teilung einer Schwingung in einem
ganz bestimmten Verhältnis eine Geometrie des Raumes erzeugt wird. Dadurch, daß die Saite an zwei Enden fest ist, hat sie eine bestimmte Länge, welche die "Grundgeometrie" definiert, und die ganzzahligen Unterteilungen erzeugen innerhalb dieser Grundgeometrie festdefinierte Verhältnisse.4
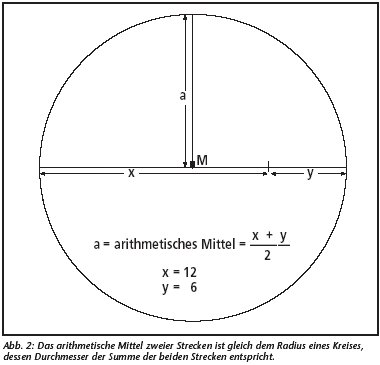 Um das zu zeigen, teilte Pythagoras die Saite in zwölf gleiche Teile, so daß beim Festhalten mit dem Finger auf der Zahl 6, der Mitte, die Oktave (wir wollen die Intervalle nach den heute üblichen Namen benennen, um nicht durcheinanderzugeraten), bei der Zahl 9 die Quarte und bei der Zahl 8 die Quinte ertönt. Die zwölf stellt die Grundschwingung dar, die den Grundton erzeugt. Wenn man nun einen Kreis zeichnet mit dem Durchmesser 12+6 (wir nennen 12 = x, 6 = y), so ist die 9 (die Quarte) genau das arithmetische Mittel (wir nennen es a), welche den Radius des Kreises darstellt (siehe Abb. 2):
Um das zu zeigen, teilte Pythagoras die Saite in zwölf gleiche Teile, so daß beim Festhalten mit dem Finger auf der Zahl 6, der Mitte, die Oktave (wir wollen die Intervalle nach den heute üblichen Namen benennen, um nicht durcheinanderzugeraten), bei der Zahl 9 die Quarte und bei der Zahl 8 die Quinte ertönt. Die zwölf stellt die Grundschwingung dar, die den Grundton erzeugt. Wenn man nun einen Kreis zeichnet mit dem Durchmesser 12+6 (wir nennen 12 = x, 6 = y), so ist die 9 (die Quarte) genau das arithmetische Mittel (wir nennen es a), welche den Radius des Kreises darstellt (siehe Abb. 2):
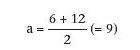
Geometrisch gesehen hat das arithmetische Mittel aber noch eine bedeutende Funktion: Es erzeugt nämlich die Seite desjenigen Quadrats, das genau den gleichen Flächeninhalt hat wie das aus den Seiten a und b gebildete Rechteck. "Mittel" heißt es also deshalb, weil es einen bestimmten Zweck erfüllt: Zu jedem beliebigen Rechteck kann man auf diese Weise das flächengleiche Quadrat finden.
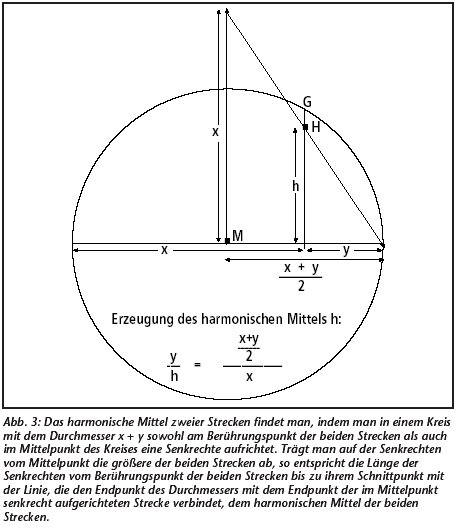 Die Quinte aber, die durch die Zahl 8 repräsentiert wird, bezeichnen die Pythagoräer als harmonisches Mittel (wir wollen es h nennen) (siehe Abb. 3):
Die Quinte aber, die durch die Zahl 8 repräsentiert wird, bezeichnen die Pythagoräer als harmonisches Mittel (wir wollen es h nennen) (siehe Abb. 3):
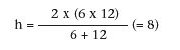
Dieses harmonische Mittel ist auch ein "Mittel zum Zweck", es zeigt nämlich die Kongruenz der Dreiecke AB1C1,
AB2C2, AB3C3, etc. Die jeweiligen Ankatheten haben untereinander immer dieselbe Proportion. (siehe Abb. 4).
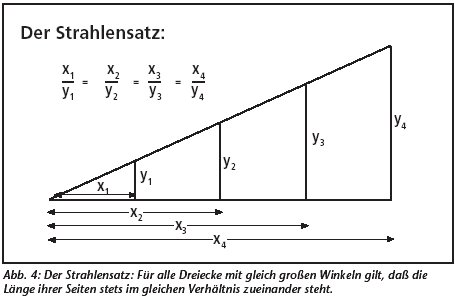 Die Lehre vom arithmetischen und harmonischen Mittel als Bezeichnung der synphonen Intervalle geht nach Zeugnissen von Philolaos, Archytas sowie Aristoteles direkt auf Pythagoras zurück. Es gilt dabei die Beziehung, welche die Pythagoräer die "vollkommenste" nannten:
Die Lehre vom arithmetischen und harmonischen Mittel als Bezeichnung der synphonen Intervalle geht nach Zeugnissen von Philolaos, Archytas sowie Aristoteles direkt auf Pythagoras zurück. Es gilt dabei die Beziehung, welche die Pythagoräer die "vollkommenste" nannten:
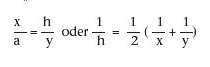
Das Harmonische Mittel hat in der Natur eine besondere Bedeutung. Der Baumeister Andrea Palladio (1508-1580) aus Vicenza geht in seinen Schriften (I quattri Libri del´archittetura) auf die Frage ein, welche Höhe ein Zimmer nach seiner Auffassung im Verhältnis zum Grundriß haben soll. In seinem "Libro Primo", Cap. XXIII, "Dell´Altezza delle Stanze", schlägt er als Raumhöhe H bei vorgegebenem Grundriß (Länge L und Seite S) drei Möglichkeiten der Proportion vor:


Vielleicht kommt diese "sinnliche" Wahrnehmung einer angenehmen architektonischen Proportion vom Sehen des menschlichen Auges: Auch hierbei spielt das harmonische Mittel eine wichtige Rolle: Wenn man einen Gegenstand sieht, so sieht man ihn
deshalb, weil die Lichtstrahlen an der Augenlinse gebeugt, dann im Brennpunkt gesammelt und als umgekehrtes (!) Bild auf der Netzhaut abgebildet werden. Bei dieser Brechung des Lichts an einer Linse (in diesem Fall der menschlichen Augenlinse) ist die Brennweite genau das Doppelte des harmonischen Mittels von Gegenstandsweite (Entfernung des Gegenstandes vom Brennpunkt) und Bildweite (Entfernung des auf der Netzhaut abgebildeten Gegenstandes vom Brennpunkt, siehe Abb. 5).
Ist diese Ähnlichkeit mit dem Hören und Empfinden schöner Intervalle nicht verblüffend ähnlich? Doch beim Sehen sehen wir nicht genau das durch die Augenlinse erzeugte Bild! Das beim Sehvorgang auf der Netzhaut erscheinende Bild steht nämlich wegen der Beugung der vom Gegenstand kommenden Strahlen auf dem Kopf, und man fragt sich: "Wie kommt es, daß wir trotzdem alles richtig herum wahrnehmen?" Wenn wir eine Tasse auf der linken Seite des Tisches sehen und greifen dorthin, so steht sie doch tatsächlich dort?!
Es ist also beim Sehen noch etwas anderes im Spiel, was man als Vorgang der Erkenntnis bezeichnen kann; ein Vorgang, der nach dem sinnlichen Eindruck oder schon währenddessen unseren Geist oder unsere Seele in Gang setzt. Und diese Erkenntnis sagt uns mit absoluter Sicherheit: Die Verhältnisse sind so und so, und das Bild, das du siehst, ist um genau 180░ gedreht! Nur deshalb sehen wir alles "richtig".
So ist es auch beim Hören: das Entscheidende für die Harmonie sind die Intervalle, die Proportionen der Töne untereinander, nicht die Töne "an sich". Dieser Unterschied war den Pythagoräern bewußt. Ist er es auch heutigen Musikern? Wir werden im nächsten Teil mit Kepler sehen, daß dies ein schwerwiegendes Paradox ist.
Auf der Grundlage dieser Erkenntnis, daß es nicht um eine lineare
Aneinanderreihung einzelner Töne geht, bauten die Pythagoräer die bekannte achtstufige Tonleiter. Jede Musik braucht eine Tonleiter, aber man darf nie vergessen, daß jede "Tonleiter" die Projektion einer höheren Geometrie ist. Das sieht man schon an der Tatsache, daß die Zwischenräume zwischen den Tönen sehr unterschiedlich sein können, je nachdem, welcher Ton die "Grundschwingung", bzw. der Referenz- oder Anfangston ist.
Wie haben Pythagoras und seine Schüler nun diese Konsonanzen angeordnet, bzw. wie werden Tonleitern konstruiert und verstehbar? Und wer oder was bestimmt die Zwischenräume? Diese Fragen wurden von den Pythagoräern im Ansatz gelöst. (Johannes Kepler ist in seinen geometrischen Erklärungen noch weiter als Archytas gelangt, und seine detaillierte Begründung für den Aufbau der Tonleiter ist bedeutend einleuchtender, aber davon später.)
Betrachten wir nun ihre Aufteilung der Saiten auf einer achtsaitigen Lyra im diatonischen Tongeschlecht (Tab. 1, linke Spalte):
Tabelle 1: die Stimmung der achtsaitigen Lyra
bei den Pythagoräern und nach Archytas |
Stimmung bei den
Pythagoräern |
Bezeichnung
der Saite |
Stimmung nach
Archytas |
|
Nete | |
| Ganzton 9:8 |
|
9:8 |
|
Paranete | |
| Ganzton 9:8 |
|
8:7 |
|
Trite | |
| "kleiner Halbton" 256:243 |
|
28:27 |
|
Paramese | |
| Ganzton 9:8 |
|
9:8 |
|
Mese | |
| Ganzton 9:8 |
|
9:8 |
|
Lichanos | |
| Ganzton 9:8 |
|
8:7 |
|
Parhypate | |
| "kleiner Halbton" 256:243 |
|
28:27 |
|
Hypate | | |
Die Aufteilung der Halb- und Ganztöne ist also:
Diatonisch: 1+1+1/2
Es gab außerdem das "Chromatische" sowie das "Enharmonische". In diesen
anderen Tongeschlechtern waren die Töne anders angeordnet:
Chromatisch: 1 1/2+1/2+1/2
Enharmonisch: 2+1/4+1/4
Dabei sind die äußeren Saiten, Nete und Hypate, sowie die beiden inneren, Mese und Paramese, jeweils fest gestimmt; Nete und Paramese sowie Mese und Hypate bildeten jeweils einen sogenannten "Tetrachord", eine reine Quarte. Zwischen Mese und Paramese lag ein ganzer Tonschritt, den sie aus dem Vergleich von Quarte 4:3 und Quinte 3:2 zu 9:8 ermittelten. Daher liegt zwischen Nete und Mese sowie Paramese und Hypate jeweils eine reine Quinte. Die inneren Saiten, also Paranete, Trite, Lichanos und Parhypate, waren variabel stimmbar - es gab für jeden Modus eine andere Verteilung der Halbton- und Ganztonschritte.
Die oben dargestellte Aufteilung der Intervalle und ihre Stimmung mit dem "kleinen Halbton" 256:243, der auch "Leimma" genannt wird, wurde laut Ptolemäus von den Kitharaspielern bevorzugt, weil sie sehr "handlich" lag. Man konnte also während des Spiels und bei einem Tonartwechsel innere Saiten ein wenig umstimmen, "temperieren", so daß ein sauberes Spiel weiter möglich war.
Die "diatonische" Stimmung der Lyra erreichte man also, wenn man sie in
reinen Quarten und Quinten stimmte. Laut Ptolemäus ("Harmonik") und Theon von Smyrna war es mit dieser Stimmung leicht möglich, zu modulieren, d.h. man konnte unter Beibehaltung der festen Stimmung von Nete, Paramese, Mese und Hypate mehrere Tonarten spielen, in dem man die inneren Töne veränderte.
 Auf die Frage, ob so etwas wie "Akkorde" und die Existenz des sog. "Leittons" überhaupt bekannt waren, muß man meiner Meinung nach mit "ja" antworten, obwohl es beinahe keine Notenbeispiele gibt, nur einige Fragmente, die aber doch so etwas erahnen lassen. Denn die durch die konsonanten Intervalle geschaffenen achtstufigen Tonleitern weisen alle den Leitton (Parhypate) mit einem besonders kleinen Abstand zur Hypate (heutige Oktave) auf (siehe Abb. 6).
Auf die Frage, ob so etwas wie "Akkorde" und die Existenz des sog. "Leittons" überhaupt bekannt waren, muß man meiner Meinung nach mit "ja" antworten, obwohl es beinahe keine Notenbeispiele gibt, nur einige Fragmente, die aber doch so etwas erahnen lassen. Denn die durch die konsonanten Intervalle geschaffenen achtstufigen Tonleitern weisen alle den Leitton (Parhypate) mit einem besonders kleinen Abstand zur Hypate (heutige Oktave) auf (siehe Abb. 6).
Dieser sogenannte "Leitton" wird deshalb so genannt, weil er stark zur Oktave drängt und damit die Aufgabe erfüllt, die benutzte Tonart eindeutig zu manifestieren. Heutige Lyrabauer sind der festen Überzeugung, daß dieses Instrument wunderbar Akkorde spielen konnte. Auch die Idee, daß die Planeten durch ihre Bewegungen eine himmlische Sphärenmusik erzeugen und alle irdische Harmonie nur ein Abbild jener sei, legt nahe, daß es mehrstimmige Musik bei den Pythagoräern gegeben haben muß. Schon allein, um Intervalle zu singen und miteinander zu vergleichen, braucht man ja mindestens zwei Stimmen!
Betrachten wir nun noch die Stimmung der Lyra, wie sie Archytas vorschlägt (Tab. 1, rechte Spalte):
Dieses ist die Stimmung im diatonischen Modus. Und die Töne der
enharmonischen und chromatischen Modi verteilte er so:
Stimmung des Archytas:
Chromatisch: 32:27 ; 243:224 ; 28:27
Enharmonisch: 5:4 ; 36:35 ; 28:27
Genauso wie bei den Pythagoräern liegt zwischen Paramese und Mese immer ein ganzer Tonschritt mit dem Verhältnis 9:8. Bei Archytas tauchen nun einige interessante und merkwürdige Intervalle bzw. Proportionen auf, wie zum Beispiel das Verhältnis 5:4, welches unsere heutige reine große Terz darstellt, sowie 28:27, welches eine verminderte kleine Terz ausmacht. Außerdem kommt noch eine entscheidende Änderung für die Praxis dazu, denn man zog nun die große Terz bei der Stimmung der Lyra hinzu, so daß zum Beispiel bei der enharmonischen Tonleiter der Lichanos mit der Mese eine reine große Terz bildete, zusätzlich zu
den reinen Quinten und Quarten zwischen Nete, Paramese, Mese und Hypate. Das ermöglichte größere Auswahl, das Instrument zu stimmen.
Die Tonleitern dieser Zeit hießen je nach Anfangston: mixolydisch (h),
lydisch (c), phrygisch (d), dorisch (e), hypolydisch (f), hypophrygisch (g) und hypodorisch (a). Bei der Überlieferung der Tonleiterbezeichnungen wurden die Namen vertauscht, so daß wir heute die sog. "Kirchentonarten" anders nennen (z.B. war die "lydische" Kirchentonart die "hypolydische" Tonart der Pythagoräer). Es war bekannt, daß jede Tonart wegen der unterschiedlich großen Zwischenräume zwischen den einzelnen Tonschritten eine unterschiedliche "Färbung" oder Ausdruck besaß. So wurde über Pythagoras folgende Anekdote
berichtet:
"Pythagoras soll auch, als er einmal in seine Arbeit vertieft war, durch spondäische Musik mit Hilfe des Aulosspielers die Raserei eines betrunkenen Jünglings aus Tauromenien beschwichtigt haben, der nachts einer Angebeteten am Hausportal des Nebenbuhlers nachschwärmte und dieses in Brand stecken wollte. Dazu hatte ihn nämlich die erregende phrygische Aulosweise angefeuert. Dem machte Pythagoras - er trieb gerade mitten in der Nacht Sternkunde - sehr schnell ein Ende, indem er dem Bläser empfahl, ins spondäische Maß überzuwechseln. Durch diesen Wechsel wurde der Jüngling alsbald besänftigt und verzog sich sittsam nach Hause..."5
Wie schon erwähnt, ist der Astronom Johannes Kepler der Lösung der
verschiedenen Paradoxe noch näher gekommen: erstens der Verbindung zwischen geometrischer Erkenntnis und der Wirkung auf die Seele, und zweitens der Tatsache, daß man nur bestimmte Intervalle als "schön" empfindet, diese in jeder Tonleiter erhalten will, aber beim Bilden der exakten Stufen einer Tonleiter Probleme bekommt, da die einzelnen Töne je nach dem Charakter der Tonleiter einmal höher, einmal tiefer liegen müssen. Er zeigte, daß der Mensch letztendlich nur mit Hilfe der Geometrie die Schönheit erkennen kann.
Fortsetzung folgt
Anmerkungen
1. Platon, Phaidros; es spricht Sokrates.
2. Siehe Curt Sachs, Handbuch der Musikinstrumentenkunde, 2. Auflage; Leipzig, Breitkopf & Härtel, 1930.
3. Aus: Jacob Grimm, "Über den Ursprung der Sprache", in
Selbstbiographie, dtv klassik, 1984, S.170/171; er bemerkt weiter über den bedeutenden Namen manudscha im Sanskrit, "...welcher auch vorzugsweise in unsrer deutschen Sprache bis auf heute sich erhalten hat, goth. (gothisch) Manniska, ahd. (althochdeutsch) Mannisco, nhd. (neuhochdeutsch) Mensch und so durch alle Mundarten; dies Wort darf zwar mit gutem Grund auf einen mythischen Ahnen Manna, Mannus, den schon Tacitus bezeugt, auf einen indischen König Manas zurückgeleitet werden, dessen
Wurzel man, d.h. denken, ist und wozu unmittelbar auch manas, μενος, Mensch fallen."
4. Dieses physikalische Paradox im Verhalten des Raumes bei
Schwingungserregungen haben später Ernst F. Chladni mit Klangplatten,
allgemeiner vor allem seine Schüler, die Brüder Wilhelm Eduard, Ernst Heinrich und Eduard Friedrich Weber an Seilen untersucht, die sie an den beiden Ufern eines Baches verankerten; durch diese Forschungen entstand ihr fundamentales Werk "Wellenlehre auf Experimenten begründet" (in: Wilhelm Weber; Werke, 5. Band; gewidmet ihrem Lehrer E.F. Chladni), welche die bisher fortgeschrittenste Theorie über die Wellenbewegung des Lichtes enthält.
5. Aus: Die Pythagoräer, B.L. van der Waerden, Artemis-Verlag, Zürich u. München, 1979.
Zurück zur Kultur-Hauptseite:
 Wie soll man einen Ton ganz genau beschreiben? Bei den ersten Lyren lagen die einzelnen Töne ziemlich weit voneinander entfernt (siehe Abb. 1), doch legte man sie mit der Zeit immer enger aneinander. Wenn Sie einmal
einen möglichst hohen Ton, dann einen möglichst tiefen und zum Schluß einen zwischen diesen beiden singen, und danach versuchen, den ersten hohen Ton wieder genau zu treffen, bekommen Sie eine Vorstellung, wie schwer es ist, sich den Klangraum so genau einzuteilen, daß es eine replizierbare Ordnung gibt. Einige Instrumentenbeispiele zeigen, daß es Hochkulturen gab, die eine sehr weitentwickelte Kenntnis vom wirklichen Aufbau des Klangraumes hatten, doch sind keine schriftlichen Erkenntnisse dieser Zeit überliefert.
Wie soll man einen Ton ganz genau beschreiben? Bei den ersten Lyren lagen die einzelnen Töne ziemlich weit voneinander entfernt (siehe Abb. 1), doch legte man sie mit der Zeit immer enger aneinander. Wenn Sie einmal
einen möglichst hohen Ton, dann einen möglichst tiefen und zum Schluß einen zwischen diesen beiden singen, und danach versuchen, den ersten hohen Ton wieder genau zu treffen, bekommen Sie eine Vorstellung, wie schwer es ist, sich den Klangraum so genau einzuteilen, daß es eine replizierbare Ordnung gibt. Einige Instrumentenbeispiele zeigen, daß es Hochkulturen gab, die eine sehr weitentwickelte Kenntnis vom wirklichen Aufbau des Klangraumes hatten, doch sind keine schriftlichen Erkenntnisse dieser Zeit überliefert.
 Um das zu zeigen, teilte Pythagoras die Saite in zwölf gleiche Teile, so daß beim Festhalten mit dem Finger auf der Zahl 6, der Mitte, die Oktave (wir wollen die Intervalle nach den heute üblichen Namen benennen, um nicht durcheinanderzugeraten), bei der Zahl 9 die Quarte und bei der Zahl 8 die Quinte ertönt. Die zwölf stellt die Grundschwingung dar, die den Grundton erzeugt. Wenn man nun einen Kreis zeichnet mit dem Durchmesser 12+6 (wir nennen 12 = x, 6 = y), so ist die 9 (die Quarte) genau das arithmetische Mittel (wir nennen es a), welche den Radius des Kreises darstellt (siehe Abb. 2):
Um das zu zeigen, teilte Pythagoras die Saite in zwölf gleiche Teile, so daß beim Festhalten mit dem Finger auf der Zahl 6, der Mitte, die Oktave (wir wollen die Intervalle nach den heute üblichen Namen benennen, um nicht durcheinanderzugeraten), bei der Zahl 9 die Quarte und bei der Zahl 8 die Quinte ertönt. Die zwölf stellt die Grundschwingung dar, die den Grundton erzeugt. Wenn man nun einen Kreis zeichnet mit dem Durchmesser 12+6 (wir nennen 12 = x, 6 = y), so ist die 9 (die Quarte) genau das arithmetische Mittel (wir nennen es a), welche den Radius des Kreises darstellt (siehe Abb. 2):
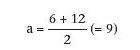
 Die Quinte aber, die durch die Zahl 8 repräsentiert wird, bezeichnen die Pythagoräer als harmonisches Mittel (wir wollen es h nennen)
Die Quinte aber, die durch die Zahl 8 repräsentiert wird, bezeichnen die Pythagoräer als harmonisches Mittel (wir wollen es h nennen) 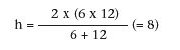
 Die Lehre vom arithmetischen und harmonischen Mittel als Bezeichnung der synphonen Intervalle geht nach Zeugnissen von Philolaos, Archytas sowie Aristoteles direkt auf Pythagoras zurück. Es gilt dabei die Beziehung, welche die Pythagoräer die "vollkommenste" nannten:
Die Lehre vom arithmetischen und harmonischen Mittel als Bezeichnung der synphonen Intervalle geht nach Zeugnissen von Philolaos, Archytas sowie Aristoteles direkt auf Pythagoras zurück. Es gilt dabei die Beziehung, welche die Pythagoräer die "vollkommenste" nannten:
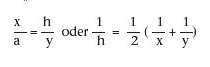


 Auf die Frage, ob so etwas wie "Akkorde" und die Existenz des sog. "Leittons" überhaupt bekannt waren, muß man meiner Meinung nach mit "ja" antworten, obwohl es beinahe keine Notenbeispiele gibt, nur einige Fragmente, die aber doch so etwas erahnen lassen. Denn die durch die konsonanten Intervalle geschaffenen achtstufigen Tonleitern weisen alle den Leitton (Parhypate) mit einem besonders kleinen Abstand zur Hypate (heutige Oktave) auf (siehe Abb. 6).
Auf die Frage, ob so etwas wie "Akkorde" und die Existenz des sog. "Leittons" überhaupt bekannt waren, muß man meiner Meinung nach mit "ja" antworten, obwohl es beinahe keine Notenbeispiele gibt, nur einige Fragmente, die aber doch so etwas erahnen lassen. Denn die durch die konsonanten Intervalle geschaffenen achtstufigen Tonleitern weisen alle den Leitton (Parhypate) mit einem besonders kleinen Abstand zur Hypate (heutige Oktave) auf (siehe Abb. 6).
