Warum ist das Schöne schön?

Abb. 1: Bildnis des Pythagoras mit Laute aus dem Chorgestühl von Jörg Syrlin d. Ä. (1425-1491) im Ulmer Münster.

Am Ende des letzten Jahres fand ein außergewöhnliches Konzert statt. Ein chinesisches Streichquartett kündigte ein außergewöhnliches Programm an: aber nicht Werke aus der chinesischen Musik, sondern Quartette von Joseph Haydn, Franz Schubert und Ludwig van Beethoven! Die Darbietung war hervorragend! Die vier Künstler spielten mit einem Temperament und einer Hingabe, daß das Publikum überwältigt war. Jeder spürte irgendwie, daß eine gemeinsame Sprache existiert, die es ermöglicht, sich gegenseitig zu begreifen und Achtung voreinander zu gewinnen: die Musik.

Die Musik ist die Weltsprache, sie rührt und begeistert Menschen auf allen Kontinenten. Mit ihren Mitteln kann sie mehr als alle Worte ausdrücken, ja sie reicht in die unmittelbaren und tiefsten Erlebnisse der menschlichen Seele, berührt alles, was im Innersten des Menschenherzens unbewußt oder nicht bedacht vorgeht. Sie ist die Heimat aller Empfindungen, doch ist sie ebenso imstande, die Seele über Zeiten und Räume über sich hinauszuheben und zu erhöhen wie keine andere Kunst. Sie läßt uns in eine bessere Welt entfliehen, die Welt der Schönheit und Wahrheit. Wie kann man sich diese Macht erklären? Woher kommt diese Kraft der Musik? Ludwig van Beethoven sagte einmal: "Musik ist eine höhere Offenbarung als alle Weisheit und Philosophie."

Oder sind es eher die gemeinsamen Gefühle, die ein Musikstück in den Menschen von Ost nach West, Nord nach Süd hervorruft, welche der Komponist beim Schreiben ausdrücken wollte, und die alle beim Hören nachempfinden? Was hätte aber die Wahrheit mit dem Gefühl zu tun?

Viele und lange Abhandlungen sind zu diesem Thema geschrieben worden. Dabei tendierte man oft dahin, die Kraft der Musik rein dem Gefühl zuzusprechen. Zum Beispiel schrieb der Hamburger Musiker und Gegenspieler J.S. Bachs, Johann Mattheson (1681-1764) unter dem Pseudonym "Aristoxenos junior": "Wir müssen bei jeder Melodie uns eine Gemütsbewegung (wo nicht mehr als Eine) zum Hauptzweck setzen", der bekannte Komponist Fermo Bellini (1801-1835): "Musica e līarte, che esprime i sentimenti e le passione col mezzo di suoni." (Die Musik ist die Kunst, die mit den Mitteln der Töne die Gefühle und Leidenschaften ausdrückt.) Der Bach-Biograph Johann Nikolaus (1749-1818) versteht unter den "Figuren der Musik... dasselbe, was sie in der Dichtkunst und Redekunst sind, nämlich der Ausdruck der unterschiedenen Arten, nach welchen sich Empfindungen und Leidenschaften äußern", und der Philosoph und Pädagoge Johann Georg Sulzer (1720-1779) schrieb: "Musik ist die Kunst, durch Töne unsre Leidenschaften auszudrücken, wie in der Sprache durch Worte" (alle Zitate aus: Hanslick, "Vom Musikalisch Schönen"; Hervorhebung durch Hanslick).

Doch wenn man sich diese Ansichten durchdenkt, kommt man in eine Zwicklage. Ist es nicht oft so, daß dieselben Musikwerke eine unterschiedliche Stimmung hervorrufen - je nachdem, wann man sie hört?

Es können also nicht nur die sinnlichen Eindrücke sein, die uns bis ins Innerste bewegen, sie sind höchstens das "Mittel". Aber was wird bewegt? Wie wird die Seele bewegt - und was ist die Seele?

Diese Fragen beschäftigen die Menschen seit Jahrtausenden. Es geht hier um das uralte Paradox, was denn der Mensch sei, wie der Körper und der Geist zusammenhängen. Dadurch, daß sie Gefühle erregt, gleichzeitig aber noch bis tief in die Seele und das bewußte (und unbewußte) Denken hineinwirkt, bildet die Musik ein Mittel, welches diese zwei Welten irgendwie miteinander in Beziehung bringt. Aber wie?

Der erste, der dieser Frage systematisch zu Leibe rückte, war Pythagoras. In der Musik (eigentlich in aller Kunst) kann man nämlich ein Phänomen beobachten, dessen Grund bis dahin niemand hinterfragt hatte: Es gibt nur eine ganz begrenzte Zahl von musikalischen Intervallen (das sind Zusammenklänge zwischen zwei gleichzeitig gespielten Tönen), die das menschliche Ohr als "schön" empfindet.

Pythagoras stellte fest, daß es hier um Proportionen geht, daß also die menschliche Seele etwas miteinander vergleicht, und er versuchte als erster, die Ursache für die Gründe unseres Schönheitsempfindens herauszufinden. Dabei machte er eine Entdeckung: die geometrisch "lebendige" Struktur des Klangraumes. Er zeigte, warum die Musik die Weltsprache ist und die Seele so sehr berührt.

Dieses Wissen machte die Weiterentwicklung der Musik im europäischen Kulturraum erst möglich. Pythagoras bewies, daß mit der Musik, wie auch durch die Geometrie und Astronomie, eben jene Gabe des Menschen ausgedrückt werden kann, die durch keine physikalische oder physiologische Untersuchung gefunden wird: das Vermögen zur schöpferischen Idee. Und er erkannte als erster, warum dieses Vermögen ewig und allen Menschen gemeinsam ist, egal welcher Hautfarbe und Abstammung, weil es nämlich der menschlichen Seele zugrundeliegt.

Ein weiterer bedeutender Schritt in der Erforschung des "Schönheitsphänomens" führt zum Astronomen Johannes Kepler. Mehr als 2 000 Jahre nach Pythagoras wendete er sich erneut diesem Paradox zu. Auf den Grundlagen der Entdeckung des Pythagoras erforschte er die Zusammenhänge der geometrischen Erkenntnisse mit dem harmonischen Grundgesetz des Aufbaus des Universums und machte dabei noch eine weitergehende, wunderbare Entdeckung über die wahren Gründe des Schönheitsempfindens des Menschen:

Wie alt nun aber die Form des menschlichen Gesangs, die sich aus konsonanten und melodischen Intervallen zusammensetzt, sein mag, die Ursachen der Intervalle blieben den Menschen verborgen, so daß man vor Pythagoras nichteinmal nach ihnen fragte. Nachdem man nun zweitausend Jahre nach ihnen suchte, bin ich, wenn ich mich nicht täusche, der erste, der sie aufs genaueste darstellt. (Johannes Kepler, Weltharmonik, S.88)

Pythagoras - "Inventor Musicae"

Über das Geburtsjahr des Pythagoras von Samos sind sich die Forscher nicht einig. Es wird auf das Jahr 600 bzw. 580 v. Chr.¹ geschätzt. In seiner Jugend verbrachte er viele Jahre - wahrscheinlich mehr als zwanzig - in Kleinasien und Ägypten, und er eignete sich dort alles Wissen an, was Priester, Magier und Weise von uralten Zeiten überliefert hatten:

Zweiundzwanzig Jahre weilte er so in Ägypten in den allerheiligsten Gemächern bei Sternkunde und Geometrie und empfing... die Einweihung in alle Göttermysterien, bis ihn die Krieger des Kambyses gefangennahmen und nach Babylonien führten. Dort verkehrte er mit den Magiern... Er ward genau unterrichtet in allem, was ihnen heilig war, erlernte die Götterverehrung in aller Vollkommenheit und gelangte bei ihnen in der Zahlenlehre, in der Musik und in den übrigen Wissenschaften ans höchste Ziel. (Aus: Iamblichos, Vita Pythagorei 19, zitiert in: Die Pythagoreer von B. L. van der Waerden, Zürich, Artemis-Verlag, 1978.)

Vieles davon ist bisher ungenügend erforscht, vieles z.B. wegen der formalen Überlieferung der geometrischen Erkenntnisse in den sogenannten "Büchern des Euklid", die fast alle den Pythagoräern zuzuschreiben sind, noch nicht in seiner ganzen Größe erkannt: Die Geometrie ist das Mittel, hochkomplizierte und mehrfach untereinander verknüpfte Vorgänge in der Natur zu begreifen und darzustellen.

Alles Wissen, eingeteilt in die vier Mathemata, basierte auf der Erkenntnis, daß das gesamte Universum nach geometrischen Verhältnissen aufgebaut ist. Ob es sich um den Aufbau des Planetensystems, den Körperbau des Menschen und aller anderen Lebewesen oder um die beste und praktischste und vorteilhafteste Art und Weise des Baus von Häusern, Brücken, Speichern und Befestigungsanlagen geht: überall stößt man auf gesetzmäßige, auf eine ganz bestimmte Weise ewig ineinander verwobene Vorgänge.

Diese "Naturgesetze" spielen sich oft in einer höheren Geometrie ab, und man muß sie auf die zwei- oder dreidimensionale Welt projizieren, um sie zu begreifen - ähnlich wie man als Autofahrer nicht immer einen riesigen Globus von der wirklichen Gestalt der Erde, auf dem alle Straßen und Autobahnen eingezeichnet sind, mit sich herumschleppt, sondern eine viel handlichere Land- und Straßenkarte, obwohl diese wegen der verschiedenen geodätischen Paradoxe nur eine zweidimensionale Projektion der Wirklichkeit ist - oder besser gesagt, ein guter "Kompromiß" (siehe Bruce Director, Die Erde vermessen, leichter gesagt als getan, in: Neue Solidarität Nr. 28-46/2000).

Was nun die Musik betrifft, so macht sie einen Teil der pythagoräischen Wissensgebiete, der Mathemata aus. Sie stellt die Lehre von der höheren Geometrie der harmonischen Tonerzeugung in der unsichtbaren Welt des Klanges dar.

Es bedeutet immer noch eine große forscherliche Anstrengung, alle die Quellen zu überprüfen und auszuwerten, die Überlieferungen der Pythagoräer über die Musik beinhalten. Einige davon muß man kritisch behandeln, wie zum Beispiel Aristoteles, der ein ganz entschiedener Gegner der Grundidee des Pythagoras über die Harmonie und Gesetzmäßigkeit des Universums war. Für ihn gab es nur einzelne "echte Fakten", aber keine zugrundeliegende Idee².

Zu den bedeutendsten und glaubwürdigsten Quellen unter den vielen ernsthaften Pythagorasforschern (siehe Fußnoten) muß man neben Nikomachus von Gerasa den Pythagoräer Archytas von Tarent (428-350 v.Chr.) zählen. Er kann zu den letzten Pythagoräern gezählt werden, die sich nach der Vertreibung noch am längsten in Süditalien gehalten haben, denn er war wegen seiner vielfältigen Fähigkeiten hochgeachtet und wurde von der Bevölkerung in Tarent siebenmal hintereinander zum Strategen gewählt. Daher beherbergte er auch viele der fliehenden und verstreuten Pythagoräer, sammelte alle ihre Erzählungen, um sie dann in einigen Büchern niederzuschreiben.

Außerdem war er selber ein Forscher, dessen weiterführende Entdeckungen in der Geometrie und auch der Musiktheorie überliefert sind. Der junge Platon unternahm im Jahre 388-387 v.Chr. eine Reise nach Süditalien, um Archytas und andere Pythagoräer zu besuchen und von ihm alles über die Lehre und Erkenntnisse des Pythagoras zu erfahren. Dieses Wissen verarbeitete er in seinem Dialog Timaios, dem "Buch über die Natur".

Worin bestand nun die musikalische Entdeckung des Pythagoras? Die gesamte Musiktheorie beruht auf dieser Entdeckung des merkwürdigen geometrischen Paradoxes der Welt der Schwingungen und Wellen. Pythagoras zeigte, daß die Klangwelt praktisch "geometrisch geordnet" ist und jegliche Tonerzeugung nur verstanden werden kann, wenn man die dadurch erzeugte geometrische Veränderung des Raumes - oder besser: der Luft - betrachtet. Deshalb sprach er auch von einer "Sphärenharmonie", einer himmlischen Musik, die durch die geometrisch angeordneten Planeten bei ihrer gemeinsamen Bewegung erzeugt wird und aus diesem Grunde nannten die Pythagoräer die irdische Musik ein Abbild der himmlischen Harmonie. Eine Erklärung ist, daß Musik immer aus einer gesetzmäßigen Bewegung verschiedener Stimmen besteht. Wie aber konnte er etwas über diese "geometrische Ordnung" wissen?

Betrachten wir folgendes Experiment, welches Pythagoras an seinem selbsterfundenen Instrument, dem Monochord, ausführte: Er spannte eine Saite auf einen länglichen Holzkasten, so daß man die durch die Schwingungen angeregten Töne lauter hören konnte. Sie können dieses Experiment selber leicht nachvollziehen, am besten mit einem Saiteninstrument, oder vielleicht auch mit einem selbstgebastelten Monochord (siehe Abb. 2). Die an beiden Enden befestigte Saite wird nun gezupft und es erklingt ein Ton, der Grundton oder die Schwingung der "leeren" Saite (siehe Abb. 3 a).

Abb. 2: Ein Monochord

Jetzt mißt man die Länge der Saite aus, halbiert sie, und drückt sie mit einem Finger genau in der Mitte auf den Kasten. Nun zupft man erneut und - es erklingt ein viel höherer Ton, was man genau erkennt, wenn man beide Töne (Grundton und Ton der halbierten Saite schnell hintereinander zupft und miteinander vergleicht. Sie klingen jedoch verblüffend ähnlich - fast wie ein Ton! Bei der halbierten Saite handelt es sich nämlich um genau die doppelte Anzahl von Schwingungen, wodurch ein Teil von zweien im Verhältnis 1 : 2 erklingt. Dieser Ton wird Oktave genannt (siehe Abb. 3 b).

Wenn man von vornherein zwei gleichlange Saiten nebeneinander auf dem Kasten anbringt, so kann man beide Töne gleichzeitig anzupfen und hört noch besser, daß die beiden Töne sehr miteinander verwandt sind und angenehm zusammenklingen (was die Pythagoräer "synphon" nannten). Außerdem kann man feststellen, daß beide Teile der heruntergedrückten Saite ein- und denselben Ton erzeugen.

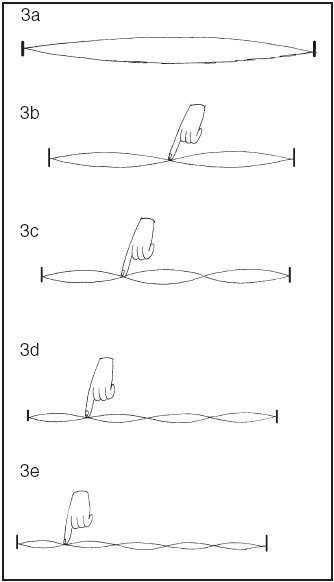
Abb. 3: schematische Darstellung der Schwingungen der Saite eines Monochords a) Schwingung der ungeteilten Saite b) Schwingung der in zwei gleiche Teile geteilten Saite (2 : 1) c) Schwingung in 3 : 2 Teilen: der restliche Teil der Saite schwingt zweigeteilt! d) Schwingung des vierten Teils der Saite (4 : 3) - die restliche Saite schwingt dreigeteilt! e) Schwingung 5 : 4. - die restliche Saite schwingt viergeteilt!

Als nächstes legte Pythagoras den Finger genau an den dritten Teil der Saite, und als er sie nun wieder anzupfte, geschah etwas merkwürdiges: die beiden Saitenteile rechts und links vom Finger schwangen nämlich nicht jeweils in einem Bogen, so wie bei der Teilung in der Mitte, sondern das längere Stück schwang in zwei Bögen, die beide genau die Länge vom kleineren Saitenstück hatten, so als hätte eine Geisterhand an einer weiteren Stelle einen Finger angelegt (siehe Abb. 3 c). Es erklingen auf diese Weise zwei Teile von dreien (Verhältnis 2 : 3). Auf der einen Seite der heruntergedrückten Saite erklingt ein Ton, der zum Grundton in einer ganz bestimmten Proportion steht. Wenn man den anderen, kürzeren Teil der heruntergedrückten Saite (Verhältnis 1 : 3) anzupft, erklingt aber ein anderer Ton, der diesem sehr ähnlich ist. Er ist dem vom Verhältnis 2 : 3 genauso ähnlich wie es der Grundton im Vergleich mit dem durch die Halbierung der Saite erzeugten Ton war. Welcher ist es wohl?³

Vergleicht man den so erzeugten Ton mit dem Grundton, der Grundschwingung, so kann man ebenfalls einen angenehmen harmonischen Klang hören.

Als nächstes teilte Pythagoras die Saite in vier Teile, und drückte mit dem Finger den vierten Teil herunter. Wiederum zeigte sich das Phänomen: die Geisterhand legte ihren Finger an die anderen zwei Enden der in vier gleiche Teile geteilte Saite (siehe Abb. 3 d)! Hier erklingt nun also auf der einen Seite des Fingers der dritte Teil von insgesamt vier Teilen, also das Verhältnis 3 : 4. Wie man hören kann, klingt auch dieser Ton verglichen mit der Ausgangsschwingung der ganzen Saite (dem Grundton) recht angenehm zusammen. Wenn man wieder den kleinen anderen Teil (Verhältnis 1 : 4) anzupft, erklingt ein weiterer Ton, der uns sicher auch angenehm im Zusammenklang der beiden anderen vorkommt.

Alle diese so gefundenen Schwingungen, die sich aus ganzzahligen Unterteilungen einer Saite ergeben, bilden für unser Ohr jeweils einen "schön" klingenden Zusammenklang mit der leeren Ausgangssaite, deshalb nannten die Pythagoräer ihn "synphon". Sie können in dem Experiment selber nachvollziehen, daß man diese Zusammenklänge (oder Intervalle) mit Recht als "schön" bezeichnen kann, denn sobald man die Saite an einer beliebig anderen Stelle, die keine geradzahlige Unterteilung darstellt, herunterdrückt und dann diesen Ton zusammen mit dem Grundton erklingen läßt, so hört man einen Klang, denn man wirklich als "schief" und häßlich bezeichnen kann.

Wir werden im weiteren noch die höhere geometrische Ursache verstehen, warum die ganzzahligen Teilungen mit der Grundsaite so gut zusammenklingen. Wenn man genau hinhört, so bemerkt man zusätzlich, daß alle Töne innerhalb des von Grundton und Oktave aufgespannten Klangraumes bzw. zwischen der Schwingung der ganzen Saite und ihrer doppelten Schwingung liegen, also ihre Höhe nicht über die doppelte Schwingung (Oktave) hinausgeht.

Heute nennen wir die doppelte Schwingung "Oktave", die Schwingung 2 : 3 Quinte und die Schwingung 3 : 4 Quarte. Warum wohl? Wie die einzelnen Töne bei den Pythagoräern und die Saiten der Lyra benannt wurden, werden wir im folgenden sehen. Auf jeden Fall waren dies die vier Intervalle, deren synphonen Klang Pythagoras mit dem Monochord demonstrierte.

Genauso wie mit der Vierteilung kann man aber das Experiment der Saitenteilung weiterführen und die Saite in fünf gleiche Teile teilen. Drückt man nun den fünften Teil mit dem Finger auf den Kasten, so erklingt das Verhältnis 4 : 5, welches bei Pythagoras den Quellen nach noch nicht bekannt war, aber von Archytas bereits benutzt wurde (siehe Abb. 3 e). Dieser Archytas von Tarent entwickelte noch weiterführende Ideen über die musikalische Harmonie. Er erkannte auch noch andere synphone Intervalle, wie zum Beispiel die heutige "kleine Terz", welche beim Schwingen der Saite im Verhältnis 4 : 5 erklingt. Im weiteren Verlauf der Musikentwicklung wurden noch drei andere Intervalle als "synphon" erkannt, welche sich ebenfalls als ganzzahlige Unterteilungen der Saiten erwiesen haben. Ob die Pythagoräer diese Teilungen (5 : 6 für die kleine Terz, 3 : 5 für die große, 5 : 8 für die kleine Sexte) bereits kannten, wissen wir heute nicht.

Bedeutet das alles nun, daß die Musik rein geometrisch erklärbar ist, alle Empfindungen der Seele erklärbar sind durch schnöde Mathematik? Gott bewahre! Doch was für eine Bedeutung haben diese Saitenteilungen, auf welche Weise begründen sie die geometrische Anordnung der Klangwelt? Ist denn die ganze Musik durch "Rechnerei" erklärbar? Wie soll man sich dann aber die Wirkung auf den Menschen bis in seine innersten Regungen der Seele vorstellen? Hängen etwa geometrische Vorgänge mit der Seele irgendwie zusammen? Oder wie ist das zu erklären? Was ist denn eigentlich die Seele?

Fortsetzung folgt

1. Mehr über Pythagoras findet man in "Neue Solidarität" 22 und 23/2004 "Wer war Pythagoras?" (1. u. 2. Teil) und "Der Satz des Pythagoras - mehr als nur eine öde Formel".

2. Francesco Petrarca, der Begründer der Renaissance, der als erster die Übersetzung der Alten, wie Platon und Aristoteles, anregte, sagte treffend über Aristoteles: "Ich habe, wenn ich mich nicht sehr täusche, alle ethischen Bücher des Aristoteles gelesen... Ich bin durch diese Bücher gelehrter, aber nicht besser geworden, wie es sich gehört hätte. Ich habe es oft bei mir selbst und anderen gegenüber beklagt, daß jener Kernpunkt der Philosophie, den er selbst im ersten Buch seiner Ethik erwähnt, bei Aristoteles so wenig betont wird: daß wir nämlich nicht so sehr viel wissen als vielmehr besser werden sollen. Ich sehe wohl, daß er das Wesen der Tugend ganz vortrefflich erklärt und sehr scharf und eingehend die Eigenschaften der Tugend und des Lasters behandelt. Aber wenn ich das gelernt habe, so weiß ich ein ganz klein wenig mehr, als ich vorher wußte, ich selbst aber, meine Seele und mein Wille sind ganz dieselben geblieben wie zuvor. Es ist ein großer Unterschied, ob ich etwas weiß, oder ob ich es liebe; ob ich es verstehe, oder ob ich nach ihm strebe." (Zitat aus dem Dichterpflänzchen-Programm über Petrarca von Lutz Schauerhammer, Sindīs Wenīge nur, muß Einer Vieles geben, November 2004.)

3. Wir werden in einem der nächsten Teile dieses Artikels, der sich mit Johannes Keplers Beiträgen zur Harmonielehre befaßt, diese Schwingungen genauer untersuchen, denn sie sind ein wesentlicher Faktor seiner geometrischen Entdeckungen!